|
|
@@ -3,13 +3,7 @@
|
|
|
|
|
|
В главе\insecondtext
|
|
|
|
|
|
-\section{Математическая модель упруго-хрупкого поведения тканого композита с
|
|
|
-поликристаллической матрицей}
|
|
|
-
|
|
|
-\section{Модели тканого композита с поликристаллической матрицей с периодическим
|
|
|
-и квазипериодическим расположением волокон}
|
|
|
-
|
|
|
-\subsection{Численное решение краевой задачи упругости методом конечных
|
|
|
+\section{Численное решение краевой задачи упругости методом конечных
|
|
|
элементов}
|
|
|
|
|
|
Краевая задача \eqref{eq:Eqvilibrium} -- \eqref{eq:Guck} с граничными условиями
|
|
|
@@ -54,27 +48,49 @@
|
|
|
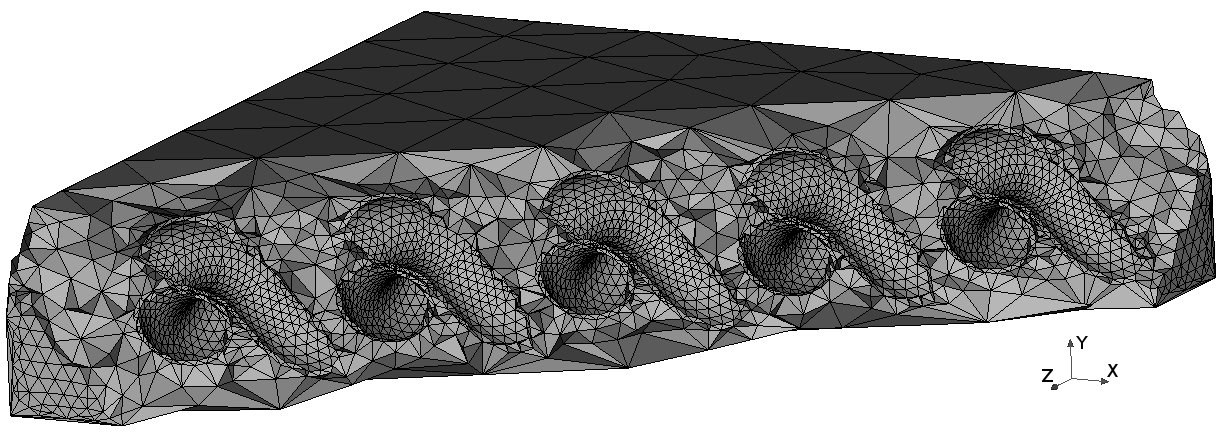
\label{fig:mesh:fibers}
|
|
|
\end{figure}
|
|
|
|
|
|
-Степень дискретизации выбиралась таким образом, чтобы чтобы полученные значения
|
|
|
-структурных перемещений, деформаций и напряжений в слое тканого композита без
|
|
|
-локальных дефектов и с несовершенствами ни качественно, ни количественно не
|
|
|
-изменялись при уменьшении характерных размеров конечных элементов.
|
|
|
+Для сопряжения конечно-элементных сеток армирующего каркаса и матрицы на этапе
|
|
|
+дискретизации выделялись <<главная>> и <<подчиненная>> поверхности. На этапе
|
|
|
+расчета узловые точки <<подчиненной>> поверхности (например, принадлежащие
|
|
|
+матрице) проецировались на те ближайшие конечные элементы, грани которых
|
|
|
+расположены на <<главной>> поверхности, и считались принадлежащими этим
|
|
|
+элементам. Перемещения точек <подчиненной>> поверхности заменялись перемещениями
|
|
|
+их проекций на элемент <<главной>> поверхности \cite{bib:code-aster:contact}.
|
|
|
+
|
|
|
+Модуль Юнга $E_f = 280$~ГПа и коэффициент Пуассона $\nu_f = 0{,}20$
|
|
|
+волокон соответствовали данным работы \cite{bib:tarnapolsky}.
|
|
|
+Упругие модули поликристаллической матрицы были выбраны следующими: $E_m
|
|
|
+= 0{,}28$~ГПа и коэффициент Пуассона $\nu_m = 0,40$.
|
|
|
+
|
|
|
+\section{Тестирование математической модели тканого композита с искривленными
|
|
|
+волокнами}
|
|
|
+
|
|
|
+Для проверки корректности построения математической модели решалась задача по
|
|
|
+определению напряженно-деформированного состояния при двухосном
|
|
|
+равнокомпонентном деформировании слоя тканого композита с искривленными
|
|
|
+волокнами для сеток с разным количеством конечных элементов и проводилось
|
|
|
+сравнение значений интенсивностей напряжений $\sigma_I$ в точке, находящейся
|
|
|
+в геометрическом центре слоя тканого композита с бездефектной идеальной
|
|
|
+периодической структурой. Такие же задачи решались для модели слоя тканого
|
|
|
+композита с дефектом в виде туннельной поры, для случаев когда полость,
|
|
|
+возникающая в следствие дефекта доуплотняется материалом связующего или
|
|
|
+остается незаполненной.
|
|
|
|
|
|
-Из таблицы~{\ref{tab:convergence}}, в которой показана зависимость максимальных
|
|
|
-интенсивностей напряжений от количества конечных элементов, видно, что
|
|
|
-расхождение между двумя последними строками не превышает $1\%$. Это говорит о
|
|
|
-достаточной степени дискретизации модели.
|
|
|
+Зависимость интенсивностей напряжений в точке, находящейся в центре слоя
|
|
|
+тканного композита от количества конечных элементов показана в таблице
|
|
|
+\ref{tab:convergence}.
|
|
|
|
|
|
\begin{table}[ht!]
|
|
|
- \caption{Зависимость максимальных интенсивностей напряжений от количества
|
|
|
- \newline конечных элементов}
|
|
|
+ \caption{Зависимость интенсивностей напряжений от количества конечных
|
|
|
+элементов}
|
|
|
|
|
|
\begin{tabular}{|c|c||c|c||c|c|}
|
|
|
\hline
|
|
|
\multicolumn{2}{|p{5cm}||}{Идеальная периодическая структура}&
|
|
|
- \multicolumn{2}{|p{5cm}||}{Тунельная пора}&
|
|
|
- \multicolumn{2}{|p{5cm}|}{Туннельная пора, доуплотненная матрицей} \\
|
|
|
+ \multicolumn{2}{|p{5cm}||}{Туннельная пора}&
|
|
|
+ \multicolumn{2}{|p{5cm}|}{Туннельная пора, доуплотненная материалом
|
|
|
+связующего} \\
|
|
|
\hline
|
|
|
- $C$ & $\sigma_{max}$ & $C$ & $\sigma_{max}$ & $C$ & $\sigma_{max}$ \\
|
|
|
+ $C$ & $\sigma_{I}$ & $C$ & $\sigma_{I}$ & $C$ & $\sigma_{I}$ \\
|
|
|
\hline
|
|
|
\hline
|
|
|
218 207 & 33.6 & 213 381 & 38.0 & 194 196 & 37.9 \\
|
|
|
@@ -89,6 +105,28 @@
|
|
|
\label{tab:convergence}
|
|
|
\end{table}
|
|
|
|
|
|
+Из таблицы видно, что расхождение между интенсивностями напряжений в двух
|
|
|
+последних вычислительных экспериментах не превышает $1\%$, что может
|
|
|
+свидетельствовать о достаточной степени дискретизации модели.
|
|
|
+
|
|
|
+Распределения интенсивностей напряжений в слое тканого композита с идеальной
|
|
|
+периодической структурой, полученные в ходе решения задачи показаны на
|
|
|
+рис.~\ref{fig:vmis_v1_s1}.
|
|
|
+
|
|
|
+\begin{figure}[ht]
|
|
|
+ \includegraphics[width=15cm]{vmis_v1_s1}
|
|
|
+ \caption{Поля интенсивности напряжений в слое тканого композита с идеальной
|
|
|
+периодической структурой}
|
|
|
+ \label{fig:vmis_v1_s1}
|
|
|
+\end{figure}
|
|
|
+
|
|
|
+Из рисунка видно, что распределение искомых полей в рассматриваемом случае
|
|
|
+удовлетворяют условиям симметрии и периодичности геометрической модели и
|
|
|
+приложенной внешней нагрузке, что говорит о корректно построенной
|
|
|
+геометрической модели и корректности полученного численного решения.
|
|
|
+Максимальных значений интенсивность напряжений достигает в местах наибольшей
|
|
|
+кривизны волокон.
|
|
|
+
|
|
|
Параметры конечно-элементной сетки, удовлетворяющие условиям неизменности
|
|
|
качественных и количественных характеристик для моделей с различными видами
|
|
|
дефектов, а также для модели с идеальной периодической структурой представлены
|
|
|
@@ -121,28 +159,8 @@
|
|
|
\label{tab:discr}
|
|
|
\end{table}
|
|
|
|
|
|
-Модуль Юнга $E_f = 280$~ГПа и коэффициент Пуассона $\nu_f = 0{,}20$
|
|
|
-волокон соответствовали данным работы \cite{bib:tarnapolsky}.
|
|
|
-Упругие модули поликристаллической матрицы были выбраны следующими: $E_m
|
|
|
-= 0{,}28$~ГПа и коэффициент Пуассона $\nu_m = 0,40$.
|
|
|
-
|
|
|
-Распределения интенсивностей напряжений в слое тканого композита с идеальной
|
|
|
-периодической структурой, полученные в ходе решения задачи показаны на
|
|
|
-рис.~\ref{fig:vmis_v1_s1}.
|
|
|
-
|
|
|
-\begin{figure}[ht]
|
|
|
- \includegraphics[width=15cm]{vmis_v1_s1}
|
|
|
- \caption{Поля интенсивности напряжений в слое тканого композита с идеальной
|
|
|
-периодической структурой}
|
|
|
- \label{fig:vmis_v1_s1}
|
|
|
-\end{figure}
|
|
|
-
|
|
|
-Из рисунка видно, что распределение искомых полей в рассматриваемом случае
|
|
|
-удовлетворяют условиям симметрии и периодичности геометрической модели и
|
|
|
-приложенной внешней нагрузке, что говорит о корректно построенной
|
|
|
-геометрической модели и корректности полученного численного решения.
|
|
|
-Максимальных значений интенсивность напряжений достигает в местах наибольшей
|
|
|
-кривизны волокон.
|
|
|
+\section{Модели тканого композита с поликристаллической матрицей с периодическим
|
|
|
+и квазипериодическим расположением волокон}
|
|
|
|
|
|
\subsection{Коэффициенты концентрации напряжений}
|
|
|
|