|
|
@@ -0,0 +1,441 @@
|
|
|
+\chapter{Теория деформаций}
|
|
|
+\label{c1}
|
|
|
+
|
|
|
+\section{Введение}
|
|
|
+
|
|
|
+Описание деформации тела связано с изучением кинематики материала. Материал при деформации рассматривается как совокупность точек, взаимное расположение которых изменяется в результате физических воздействий на материал или тело. Гипотеза сплошности приводит к тому, что соседние материальные частицы, которые были смежными в естественном начальном состоянии остаются смежными и в деформированном состоянии. Это физическая интерпретация того, что изменение материала происходит непрерывно, при этом никакая материальная частица не превращается в объем исчезающе малый или бесконечно большой.
|
|
|
+
|
|
|
+При деформировании сплошной среды все материальные частицы могут получать перемещения. В основе классической теории деформаций лежит метод описания кинематики сплошной среды с помощью вычисления удлинений линейных элементов и изменений углов между линейными элементами, имеющими общую вершину.
|
|
|
+
|
|
|
+\begin{description}
|
|
|
+ \item[Линейный элемент] --- отрезок, соединяющий 2 бесконечно близкие точки.
|
|
|
+\end{description}
|
|
|
+
|
|
|
+Способ описания кинематики сплошной среды, связанный с линейными элементами является предпочтительным по отношению к описанию полных перемещений всех точек материала, поскольку позволяет исключить перемещение точки, не связанные с изменением внутреннего состояния.
|
|
|
+
|
|
|
+Если линейные элементы в естественном начальном состоянии в искомой точке были направлены вдоль осей координат $X_k$ , то удлинения этих элементов вычисляются следующим образом:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:lambda}
|
|
|
+ \Lambda_{\nu}^{(k)} = 1 + E_{\nu}^{(k)} = \sqrt{1+2 \cdot E_{kk}}.
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+где $\Lambda_{\nu}^{(k)}$ --- удлинение линейного элемента, направленного вдоль оси $X_k$,
|
|
|
+$E_{\nu}^{(k)}$ --- относительное удлинение линейного элемента, направленного вдоль оси $X_k$,
|
|
|
+$E_{kk}$ --- диагональные компоненты тензора деформаций $E_{ij}$, которые можно вычислить, если известна векторная функция перемещений всех точек среды.
|
|
|
+
|
|
|
+$\overrightarrow{U} = \overrightarrow{U}(X_1,X_2,X_3)$ --- непрерывная и дифференцируемая функция координат. При этом $E_{ij}$ связан с проекциями вектора перемещений $U$ следующим соотношением:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:E_ij}
|
|
|
+ \begin{array}{ll}
|
|
|
+ E_{ij}(X_1,X_2,X_3) = & \frac{1}{2} \left[ \frac{\partial U_i(X_1,X_2,X_3)}{\partial X_j} +
|
|
|
+ \frac{\partial U_j(X_1,X_2,X_3)}{\partial X_i} + \right.\\
|
|
|
+ &\left. \frac{\partial U_m(X_1,X_2,X_3)}{\partial X_i} \cdot
|
|
|
+ \frac{\partial U_m(X_1,X_2,X_3)}{\partial X_j} \right].
|
|
|
+ \end{array}
|
|
|
+\end{equation}
|
|
|
+
|
|
|
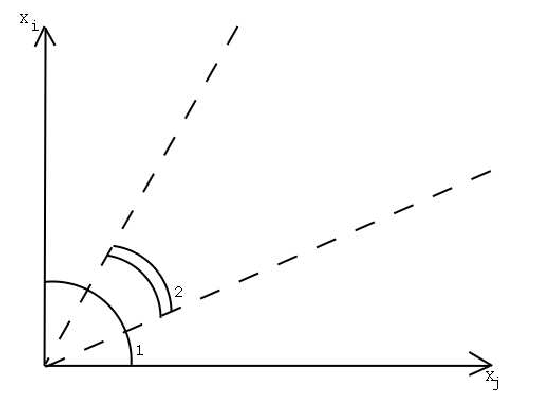
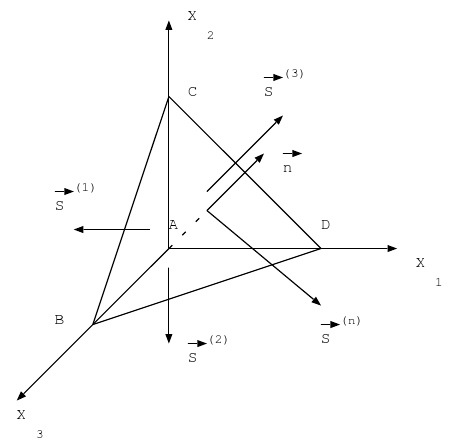
+Изменения углов вычисляется следующим образом: пусть один линейный элемент в некоторой точке в естественном состоянии направлен вдоль оси $X_i$, а другой --- вдоль оси $X_j$.
|
|
|
+
|
|
|
+% Pict1
|
|
|
+\begin{figure}[h]
|
|
|
+ \centering
|
|
|
+ \includegraphics[width = 0.7\textwidth]{picts/pict1.png}
|
|
|
+\caption{Изменения углов}
|
|
|
+\label{fig:angles}
|
|
|
+\end{figure}
|
|
|
+
|
|
|
+1 --- $\Theta_{ij}$ --- угол между элементами в не деформируемом состоянии;
|
|
|
+2 --- $\vartheta_{ij}$ --- угол в деформированном состоянии;
|
|
|
+$\gamma_{ij} = \Theta_{ij} − \vartheta_{ij}$ --- изменение угла между линейными элементами с одной общей вершиной.
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:gamma_ij}
|
|
|
+ \sin(\gamma_{ij}) = \frac{2 \cdot E_{ij}}{\Lambda_{\nu}^{(i)} \cdot \Lambda_{\nu}^{(j)}}.
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+Из гипотезы о твердости материала следует, что перемещение точек при деформировании являются малыми, также малыми величинами являются относительные удлинения линейных элементов и изменение углов между линейными элементами\footnote{По сравнению с нулем.}.
|
|
|
+
|
|
|
+В силу малости производных от перемещений, вследствие твердости материалов и тел, произведением производных в выражении (\ref{c1:E_ij}) можно пренебречь по отношению к самим производным. \marginpar{$\alpha << 1$;\\ $\alpha \sim (0.01 \div 0.001)$ => в выражении $\alpha + \alpha^2$ величиной $\alpha^2$ можно пренебречь.} И тогда для твердых тел и материалов выражение (\ref{c1:E_ij}) преобразуется к виду:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:E_ij_sim}
|
|
|
+ E_{ij} = \frac{1}{2} \cdot \left( \frac{\partial U_i}{\partial X_j} + \frac{\partial U_j}{\partial X_i} \right).
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+При этом тензор $E_{ij}$ является малой величиной порядка $\alpha$.
|
|
|
+
|
|
|
+$$
|
|
|
+ \sqrt{1 + 2 \cdot E_{kk}} \approx \sqrt{1 + 2 \cdot E_{kk} + E_{kk}^2} = \sqrt{(1 + E_{kk})^2} = 1 + E_{kk}.
|
|
|
+$$
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:lambda_nu_k}
|
|
|
+ \Lambda_{\nu}^{k} = 1 + E_{\nu}^{(k)} = 1 + E_{kk}.
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+В формуле (\ref{c1:lambda_nu_k}) величины $E_{kk}$ являются диагональными элементами тензора деформации $E_{ij}$ и имеют однозначный физический смысл: являются относительными удлинениями линейных элементов, направленных до деформации вдоль осей координат $X_k$.
|
|
|
+
|
|
|
+С учетом малых величин\footnote{$\alpha$ мала по сравнению с 1, $\sin \gamma \approx \gamma$.} выражение (\ref{c1:gamma_ij}) преобразуется к виду:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:gamma_sim}
|
|
|
+ \gamma_{ij} = 2 \cdot E_{ij}, \qquad i \neq j.
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+Из формулы (\ref{c1:gamma_sim}) видно, что недиагональные элементы тензора $E_{ij}$ , в случае малости деформаций, также имеют физический смысл: они равны половине величины изменения прямого угла, который в недеформированном состоянии был образован линейными элементами, направленными вдоль осей $X_i$ и $X_j$.
|
|
|
+
|
|
|
+\section{Малые деформации}
|
|
|
+
|
|
|
+Если перемещения и их производные считать малыми величинами, то при описании перемещений точек среды функциями компонент $U_i(X_1, X_2, X_3)$ вектора перемещений $\overrightarrow{U} = (U_1, U_2, U_3)$ можно вывести тензор, который называется тензором малых деформаций и обозначается как $\varepsilon_{ij} = E_{ij}$ (тензор деформаций Коши):
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:tenzor_koshi}
|
|
|
+ \varepsilon_{ij} = \frac{1}{2} \left[ \frac{\partial U_i}{\partial X_j} + \frac{\partial U_j}{\partial X_i} \right].
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+Из выражения (\ref{c1:tenzor_koshi}) следует, что тензор $\varepsilon_{ij}$ является симметричным\footnote{То есть $\varepsilon_{ij} = \varepsilon_{ji}$.}. Само выражение (\ref{c1:tenzor_koshi}), которое связывает перемещения точек с тензором деформаций называется геометрическим соотношением Коши или геометрическим соотношением теории малых деформаций. Диагональные элементы тензора $\varepsilon_{ij}$ вычисляются следующим образом:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:epsilon_ii}
|
|
|
+ \varepsilon_{11} = \frac{\partial U_1}{\partial X_1}, \qquad
|
|
|
+ \varepsilon_{22} = \frac{\partial U_2}{\partial X_2}, \qquad
|
|
|
+ \varepsilon_{33} = \frac{\partial U_3}{\partial X_3}.
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+Для не диагональных элементов:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:epsilon_ij}
|
|
|
+ \begin{array}{l}
|
|
|
+ \varepsilon_{12} = \varepsilon_{21} = \frac{1}{2} \left[ \frac{\partial U_1}{\partial X_2} + \frac{\partial U_2}{\partial X_1} \right], \\
|
|
|
+ \varepsilon_{13} = \varepsilon_{31} = \frac{1}{2} \left[ \frac{\partial U_1}{\partial X_3} + \frac{\partial U_3}{\partial X_1} \right], \\
|
|
|
+ \varepsilon_{23} = \varepsilon_{32} = \frac{1}{2} \left[ \frac{\partial U_2}{\partial X_3} + \frac{\partial U_3}{\partial X_2} \right].
|
|
|
+ \end{array}
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+Поскольку $\varepsilon_{ij}$ является тензором второго ранга, то при повороте системы координат вокруг своего центра компоненты тензора деформаций в новой системе координат вычисляются по следующей формуле:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:epsilon_rotate}
|
|
|
+ \varepsilon_{ij}' = \alpha_{im} \alpha_{jn} \varepsilon_{mn}.
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+Где $\varepsilon_{mn}$ --- компоненты тензора в исходной системе координат, а $\alpha_{pq}$ --- матрица поворота системы координат:
|
|
|
+
|
|
|
+$$
|
|
|
+\alpha_{pq} = \left(
|
|
|
+\begin{array}{ccc}
|
|
|
+ \cos(\widehat{X'_1,X_1}) & \cos(\widehat{X'_1,X_2}) & \cos(\widehat{X'_1,X_3}) \\
|
|
|
+ \cos(\widehat{X'_2,X_1}) & \cos(\widehat{X'_2,X_2}) & \cos(\widehat{X'_2,X_3}) \\
|
|
|
+ \cos(\widehat{X'_3,X_1}) & \cos(\widehat{X'_3,X_2}) & \cos(\widehat{X'_3,X_3})
|
|
|
+\end{array} \right)
|
|
|
+$$
|
|
|
+
|
|
|
+Для любого произвольно заданного тензора деформаций $\varepsilon_{ij}$ можно найти также положение осей координат (то есть такую новую систему координат по отношению к исходной), что тензор деформаций в новой системе координат будет иметь только диагональные компоненты.
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:epsilon_diag}
|
|
|
+ \varepsilon_{ij} = \left(
|
|
|
+ \begin{array}{ccc}
|
|
|
+ \varepsilon_{11} & \varepsilon_{12} & \varepsilon_{13} \\
|
|
|
+ \varepsilon_{21} & \varepsilon_{22} & \varepsilon_{23} \\
|
|
|
+ \varepsilon_{31} & \varepsilon_{32} & \varepsilon_{33}
|
|
|
+ \end{array} \right) \rightarrow
|
|
|
+ \varepsilon'_{ij} = \left(
|
|
|
+ \begin{array}{ccc}
|
|
|
+ \varepsilon'_{11} & 0 & 0 \\
|
|
|
+ 0 & \varepsilon'_{22} & 0 \\
|
|
|
+ 0 & 0 & \varepsilon'_{33}
|
|
|
+ \end{array}\right).
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+Эти компоненты называются главными линейными деформациями\footnote{Для произвольного тензора диагональные компоненты называются линейными деформациями, а недиагональные --- деформациями сдвига.}.
|
|
|
+
|
|
|
+Для тензора малых деформаций, также как и для любого симметричного тензора второго ранга, существуют инварианты, то есть величины, вычисляемые через компоненты тензора и не изменяющие свои значения при повороте системы координат. Для произвольного поворота системы координат вокруг центра, инварианты тензора деформаций имеют вид:
|
|
|
+
|
|
|
+$$
|
|
|
+ \begin{array}{l}
|
|
|
+ I_{\varepsilon}^{(1)} = \delta_{ij} \cdot \varepsilon_{ij} = \varepsilon_{11} + \varepsilon_{22} + \varepsilon_{33}, \\
|
|
|
+ I_{\varepsilon}^{(1)} = \frac{V_1 - V}{V}, \\
|
|
|
+ I_{\varepsilon}^{(2)} = \varepsilon_{ij} \cdot \varepsilon_{ji}, \\
|
|
|
+ I_{\varepsilon}^{(3)} = \varepsilon_{ik} \cdot \varepsilon_{km} \cdot \varepsilon{im}.
|
|
|
+ \end{array}
|
|
|
+$$
|
|
|
+
|
|
|
+$I_{\varepsilon}^{(1)}$ --- изменение объема материальной частицы в деформированном состоянии.
|
|
|
+
|
|
|
+При повороте системы координат вокруг одной из осей количество инвариантов увеличивается. Например, вокруг оси $X_3$:
|
|
|
+
|
|
|
+$$
|
|
|
+ \begin{array}{l}
|
|
|
+ I_{\varepsilon}^{(1)} = \varepsilon_{11} + \varepsilon_{22}, \\
|
|
|
+ I_{\varepsilon}^{(2)} = \varepsilon_{33}, \\
|
|
|
+ I_{\varepsilon}^{(3)} = \varepsilon_{13}^2 + \varepsilon_{23}^2, \\
|
|
|
+ I_{\varepsilon}^{(4)} = (\varepsilon_{11} - \varepsilon_{22})^2 + 4\varepsilon_{12}^2.
|
|
|
+ \end{array}
|
|
|
+$$
|
|
|
+
|
|
|
+Кинематически допустимым полем перемещений для материала называются однозначные непрерывные и дифференцируемые функции компонент вектора перемещений точек среды. Если же рассматривается область, ограниченная поверхностью, и на всей этой поверхности или на ее части заданы перемещения точек, то на кинематически допустимое поле перемещений накладывается дополнительное условие, а именно: функции компонент тензора перемещений на границе области должны принимать заданные значения.
|
|
|
+
|
|
|
+\section{Малые вращения}
|
|
|
+
|
|
|
+Тензор $\varepsilon_{ij}$ связан с перемещениями:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:epsilon_u}
|
|
|
+ \varepsilon_{ij} = \frac{1}{2} \cdot \left[ U_{i,j} + U_{j,i} \right].
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+В соотношении (\ref{c1:epsilon_u}) используется сокращенная тензорная форма записи производных. Само соотношение (\ref{c1:epsilon_u}) полностью эквивалентно соотношению (\ref{c1:tenzor_koshi}), в котором использована полная тензорная форма записи производных. Если независимыми переменными являются переменные $X_j = (X_1, X_2, X_3)$ и существует произвольная скалярная функция $f(X_1, X_2, X_3)$, то частные производные в цифровой индексной форме записываются: $\frac{\partial f}{\partial X_1}$, $\frac{\partial f}{\partial X_2}$, $\frac{\partial f}{\partial X_3}$, в тензорном виде: $\frac{\partial f}{\partial X_j}$, а в сокращенном виде: $f_{i,j}$.
|
|
|
+
|
|
|
+Рассмотрим наряду с симметричным тензором $\varepsilon_{ij}$ антисимметричный тензор, построенный по соотношению, аналогичному (\ref{c1:epsilon_u}):
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:omega}
|
|
|
+ \omega_{ij} = -\omega_{ji} = \frac{1}{2} \left[ U_{i,j} - U_{j,i} \right].
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+$$
|
|
|
+ \omega_{ij} = \left(
|
|
|
+ \begin{array}{ccc}
|
|
|
+ \omega_{11} & \omega_{12} & \omega_{13} \\
|
|
|
+ \omega_{21} & \omega_{22} & \omega_{23} \\
|
|
|
+ \omega_{31} & \omega_{32} & \omega_{33}
|
|
|
+ \end{array}\right) = \left(
|
|
|
+ \begin{array}{ccc}
|
|
|
+ 0 & \omega_{12} & \omega_{13} \\
|
|
|
+ -\omega_{12} & 0 & \omega_{23} \\
|
|
|
+ -\omega_{13} & -\omega_{23} & 0
|
|
|
+ \end{array}\right)
|
|
|
+$$
|
|
|
+
|
|
|
+Тензор деформаций $\varepsilon_{ij}$ имеет 9 компонент, из них 6 независимых (в силу симметрии). Антисимметричный тензор $\omega_{ij}$ тоже имеет 9 компонент, из которых независимыми являются только 3: $\omega_{12}$ , $\omega_{13}$ , $\omega_{23}$. Тензор $\omega_{ij}$ называют тензором малых вращений. Можно показать, что если при заданном поле перемещений в какой либо точке тензор деформаций $\varepsilon_{ij} = 0$\footnote{Тензор равен нулю если все его компоненты равны нулю.}, то тензор $\omega_{ij}$ задает малое вращение среды вокруг данной точки, причем окрестность среды вращается как абсолютно твердая. Это малое вращение происходит за счет деформаций других точек этой окрестности.
|
|
|
+
|
|
|
+\section{Уравнения совместности деформаций}
|
|
|
+
|
|
|
+Тензор деформаций в точке вызывает изменение геометрии элементарной частицы, выделенной вокруг этой точки. Из гипотезы сплошности следует, что смежные элементарные частицы не могут деформироваться как угодно произвольно, они должны деформироваться совместно с тем, чтобы среда и в деформированном состоянии оставалась сплошной (непрерывной). Математически это означает, что компоненты тензора деформаций $\varepsilon_{ij}$ как функции координат $\varepsilon_{ij} = \varepsilon_{ij}(X_1, X_2, X_3)$ не могут быть произвольно заданы, а должны удовлетворять некоторому условию или каким-то уравнениям, обеспечивающим сплошность среды в деформированном состоянии. Такие уравнения называют уравнениями совместности деформаций.
|
|
|
+
|
|
|
+$$
|
|
|
+ \varepsilon_{ij} = \frac{1}{2}\left( U_{i,j} + U_{j,i} \right), \qquad
|
|
|
+ \omega_{ij} = \frac{1}{2}\left( U_{i,j} - U_{j,i} \right).
|
|
|
+$$
|
|
|
+
|
|
|
+Наряду с этими тензорами можно ввести тензор относительных перемещений:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:nu_equiv}
|
|
|
+ \nu \equiv U_{i,j}.
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:nu}
|
|
|
+ \nu = \varepsilon_{ij} + \omega_{ij}.
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+Докажем тождество для произвольного тензора малых вращений.
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:omega_alpha_beta}
|
|
|
+ \omega_{\alpha \beta, \gamma} - \omega_{\alpha \gamma, \beta} = \omega_{\gamma \beta, \alpha}.
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+С использованием соотношения (\ref{c1:omega}) получим:
|
|
|
+
|
|
|
+$$
|
|
|
+ \frac{1}{2}\left( U_{\alpha,\beta} - U_{\beta,\alpha} \right)_{,\gamma} -
|
|
|
+ \frac{1}{2}\left( U_{\alpha,\gamma} - U_{\gamma,\alpha} \right)_{,\beta} =
|
|
|
+ \frac{1}{2}\left( U_{\gamma,\beta} - U_{\beta,\gamma} \right)_{,\alpha}.
|
|
|
+$$
|
|
|
+
|
|
|
+Преобразуя левую часть этого тождества получим:
|
|
|
+
|
|
|
+$$
|
|
|
+ \frac{1}{2} U_{\alpha,\beta \gamma} - \frac{1}{2} U_{\beta,\alpha \gamma} - \frac{1}{2} U_{\alpha,\gamma \beta} +
|
|
|
+ \frac{1}{2} U_{\gamma,\alpha \beta} = \frac{1}{2} U_{\gamma,\alpha \beta} - \frac{1}{2} U_{\beta,\alpha \gamma} =
|
|
|
+ \frac{1}{2} \left( U_{\gamma,\beta} - U_{\beta,\gamma} \right)_{,\alpha}.
|
|
|
+$$
|
|
|
+
|
|
|
+Для тензора относительных деформаций запишем:
|
|
|
+
|
|
|
+$$
|
|
|
+ \eta_{\alpha\beta} = \varepsilon_{\alpha\beta} + \omega_{\alpha\beta},
|
|
|
+ \eta_{\alpha\gamma} = \varepsilon_{\alpha\gamma} + \omega_{\alpha\gamma}.
|
|
|
+$$
|
|
|
+
|
|
|
+Продифференцируем первое уравнение по $\gamma$, а второе по $\beta$ и вычтем из первого уравнения второе:
|
|
|
+
|
|
|
+$$
|
|
|
+ \eta_{\alpha\beta,\gamma} - \eta_{\alpha\gamma,\beta} = \varepsilon_{\alpha\beta,\gamma} - \varepsilon_{\alpha\gamma,\beta} + \omega_{\alpha\beta,\gamma} - \omega_{\alpha\gamma,\beta}.
|
|
|
+$$
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:epsilon_alpha_beta_gamma}
|
|
|
+ \varepsilon_{\alpha\beta,\gamma} - \varepsilon_{\alpha\gamma,\beta} = -\omega_{\gamma\beta,\alpha}.
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+\marginpar{$\eta_{\alpha\beta,\gamma} = U_{\alpha,\beta\gamma}$,\\$\eta_{\alpha\gamma,\beta} = U_{\alpha,\gamma\beta}$,\\$\omega_{\alpha\beta,\gamma} - \omega_{\alpha\gamma,\beta} = \omega_{\gamma\beta,\alpha}$}
|
|
|
+
|
|
|
+Пусть в (\ref{c1:epsilon_alpha_beta_gamma}) $\alpha = \gamma$ (поскольку (\ref{c1:epsilon_alpha_beta_gamma}) справедливо для любого случая):
|
|
|
+
|
|
|
+$$
|
|
|
+ \varepsilon_{\gamma\beta,\gamma} - \varepsilon_{\gamma\gamma,\beta} = -\omega_{\gamma\beta,\gamma}.
|
|
|
+$$
|
|
|
+
|
|
|
+Для исключения $\omega_{\gamma\beta}$ из рассмотрения необходимо первое уравнение продифференцировать по $\gamma$, а второе --- по $\alpha$ и сложить эти уравнения:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:comp_def}
|
|
|
+ \varepsilon_{\gamma\beta,\gamma\alpha} + \varepsilon_{\alpha\gamma,\beta\gamma} -
|
|
|
+ \varepsilon_{\gamma\gamma,\beta\alpha} - \varepsilon_{\alpha\beta,\gamma\gamma} = 0.
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+Выражение (\ref{c1:comp_def}) называется уравнениями совместности деформаций.
|
|
|
+
|
|
|
+Основной результат уравнений (\ref{c1:comp_def}) заключается в том, что для того чтобы среда в деформированном состоянии оставалась непрерывной, ограничение или дополнительное условие накладывается на вторые производные функций $\varepsilon_{ij}(X_1, X_2, X_3)$ компонент тензора малых деформаций Коши.
|
|
|
+
|
|
|
+Для уравнений (\ref{c1:comp_def}) существуют эквивалентные формы записи, в которых используются другие системы индексов. Одной из таких эквивалентных форм является следующая:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:comp_def_1}
|
|
|
+ \varepsilon_{ik,lj} + \varepsilon_{lj,ik} - \varepsilon_{il,jk} - \varepsilon_{jk,il} = 0.
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+Другой эквивалентной формой является запись уравнений совместности деформаций с использованием трех индексов, например --- $i$, $j$, $k$:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:comp_def_2}
|
|
|
+ \varepsilon_{kk,ij} = \left(\varepsilon_{jk,i} - \varepsilon_{ij,k} + \varepsilon_{ik,j}\right)_{,k}
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+Уравнения совместности (\ref{c1:comp_def}) -- (\ref{c1:comp_def_2}) в развернутом виде с использованием цифровой индексной формы записи выглядят следующим образом:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:comp_def_full}
|
|
|
+ \begin{array}{lc}
|
|
|
+ I & \left\{
|
|
|
+ \begin{array}{ll}
|
|
|
+ \frac{\partial^2 \varepsilon_{11}}{\partial X_2 \partial X_3} = &
|
|
|
+ \frac{\partial}{\partial X_1} \left(
|
|
|
+ \frac{\partial \varepsilon_{13}}{\partial X_2} +
|
|
|
+ \frac{\partial \varepsilon_{12}}{\partial X_3} -
|
|
|
+ \frac{\partial \varepsilon_{23}}{\partial X_1} \right) \\
|
|
|
+ \frac{\partial^2 \varepsilon_{22}}{\partial X_1 \partial X_3} = &
|
|
|
+ \frac{\partial}{\partial X_2} \left(
|
|
|
+ \frac{\partial \varepsilon_{12}}{\partial X_3} +
|
|
|
+ \frac{\partial \varepsilon_{23}}{\partial X_1} -
|
|
|
+ \frac{\partial \varepsilon_{13}}{\partial X_2} \right) \\
|
|
|
+ \frac{\partial^2 \varepsilon_{33}}{\partial X_1 \partial X_2} = &
|
|
|
+ \frac{\partial}{\partial X_3} \left(
|
|
|
+ \frac{\partial \varepsilon_{23}}{\partial X_1} +
|
|
|
+ \frac{\partial \varepsilon_{13}}{\partial X_2} -
|
|
|
+ \frac{\partial \varepsilon_{12}}{\partial X_3} \right) \\
|
|
|
+ \end{array}\right. \\
|
|
|
+ II & \left\{
|
|
|
+ \begin{array}{ll}
|
|
|
+ 2\frac{\partial^2 \varepsilon_{12}}{\partial X_1 \partial X_2} = &
|
|
|
+ \frac{\partial^2 \varepsilon_{11}}{\partial X_2^2} + \frac{\partial^2 \varepsilon_{22}}{\partial X_1^2} \\
|
|
|
+ 2\frac{\partial^2 \varepsilon_{13}}{\partial X_1 \partial X_3} = &
|
|
|
+ \frac{\partial^2 \varepsilon_{11}}{\partial X_3^2} + \frac{\partial^2 \varepsilon_{33}}{\partial X_1^2} \\
|
|
|
+ 2\frac{\partial^2 \varepsilon_{23}}{\partial X_2 \partial X_3} = &
|
|
|
+ \frac{\partial^2 \varepsilon_{22}}{\partial X_3^2} + \frac{\partial^2 \varepsilon_{33}}{\partial X_3^2}
|
|
|
+ \end{array}\right.
|
|
|
+ \end{array}
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+\marginpar{В уравнениях $I$ группы, при получении их \\ из уравнений (\ref{c1:comp_def_2}) $j \neq k$.}
|
|
|
+
|
|
|
+Уравнения (\ref{c1:comp_def_full}) являются уравнениями деформаций, записанными в развернутом виде. Всего их 6 и они состоят из 2х групп --- по 3 в каждой. $I$ группа записана относительно вторых производных от линейных деформаций, а $II$ группа --- относительно вторых производных деформаций сдвига.
|
|
|
+
|
|
|
+Общая характеристика уравнений (\ref{c1:comp_def_full}): уравнения в частных производных, второго порядка, линейные, однородные, с постоянными коэффициентами, равными единице. Уравнения (\ref{c1:comp_def_full}) образуют систему уравнений, так как одни и те же компоненты тензора деформаций входят в разные уравнения.
|
|
|
+
|
|
|
+Поля деформаций, то есть совокупность независимых компонент тензора деформаций, заданных как функции координат, называются кинематически
|
|
|
+допустимыми, если они удовлетворяют во всех точках среды уравнениям совместности деформаций.
|
|
|
+
|
|
|
+\section[Вычисление перемещений по полю деформаций]{Вычисление перемещений по \\ заданному полю деформаций}
|
|
|
+
|
|
|
+Если перемещения точек среды заданы как функции координат $U_i = $ \\ $U_i(X_1, X_2, X_3)$, то поле деформаций $\varepsilon_{ij} = \varepsilon_{ij}(X_1, X_2, X_3)$ может быть вычислено непосредственно по геометрическим соотношениям Коши:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:strain_field}
|
|
|
+ \varepsilon_{ij} = \frac{1}{2} \left( \frac{\partial U_i}{\partial X_j} + \frac{\partial U_j}{\partial X_i} \right).
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+Рассмотрим обратную задачу: пусть задано поле деформаций, то есть заданы функции компонент тензора деформаций как непрерывные и дифференцируемые. Будем считать, что поле деформаций является кинематически допустимым, то есть функции $\varepsilon_{ij} = \varepsilon_{ij}(X_1, X_2, X_3)$ заданы таким образом, что удовлетворяются все уравнения совместности деформаций (\ref{c1:comp_def_full}). Если находить
|
|
|
+перемещения по заданным деформациям $\varepsilon_{ij}$, то геометрические соотношения Коши (\ref{c1:strain_field}) следует рассматривать как систему уравнений относительно неизвестных функций $U_i$ при заданных функциях $\varepsilon_{ij}$. Причем, если к неизвестным функциям $U_i$ добавить постоянные перемещения $U_i^{*} = const$\footnote{То есть перемещения тела или среды как абсолютно жестких.} , то такие суммарные перемещения $U_i + U_i^{∗}$ тоже будут являться решением уравнений (\ref{c1:strain_field}).
|
|
|
+
|
|
|
+Для исключения неопределенности в вычислении перемещений выберем некоторую точку $M^0(X_1^0, X_2^0, X_3^0)$, находящуюся внутри среды или тела и зададим в этой точке перемещения $U_i = U_i^0$ и малое вращение $\omega_{ij} = \omega_{ij}$.
|
|
|
+
|
|
|
+Для тензора относительных перемещений $\eta_{ij}$ ранее было получено, что
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:eta_ij}
|
|
|
+ \eta_{ij} = \frac{\partial U_i}{\partial X_j} = \varepsilon_{ij} + \omega_{ij}.
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+Уравнения (\ref{c1:eta_ij}) выполняются в каждой точке среды или тела и, интегрируя их, получим выражения для перемещений $U_i$ в произвольной точке:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:movement}
|
|
|
+ U_i\left(X'_1,X'_2,X'_3\right) = U_i^0 + \int_{M^0}^{M'} (\varepsilon_{ij} + \omega_{ij})dX_j.
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+В выражении (\ref{c1:movement}) интеграл берется по произвольной траектории $M^0$ --- $M'$, полностью лежащей внутри рассматриваемой среды или тела.
|
|
|
+
|
|
|
+Для вычисления перемещений из выражения (\ref{c1:movement}) необходимо исключить поле малых вращений $\omega_{ij}$, так как оно неизвестно. Разобьем интеграл на два слагаемых:
|
|
|
+
|
|
|
+\marginpar{Используем формули интегрирования по частям: $\int_{X_0}^{X_1} PdQ = \\ PQ|_{X_0}^{X_1} - \int_{X_0}^{X_1}QdP$}
|
|
|
+
|
|
|
+$$
|
|
|
+\begin{array}{ll}
|
|
|
+ \int_{M^0}^{M'}\omega_{ij}dX_j \rightarrow dX_j = & -d(X'_j - X_j); \\
|
|
|
+ \int_{M^0}^{M'}\omega_{ij}dX_j = & -\int_{M^0}^{M'}\omega_{ij}d(X'_j - X_j) = \\
|
|
|
+ -\left.\omega_{ij}(X'_j - X_j)\right\|_{M^0}^{M'} + & \int_{M^0}^{M'}(X'_j - X_j)d\omega_{ij} = \\
|
|
|
+ \omega^0(X'_j - X_j^0) + & \int_{M^0}^{M'}(X'_j - X_j)d\omega_{ij}.
|
|
|
+\end{array}
|
|
|
+$$
|
|
|
+
|
|
|
+В последнем выражении вместо неизвестного поля малых вращений присутствует дифференциал этого поля $d\omega_{ij}$, который может быть записан:
|
|
|
+
|
|
|
+$$
|
|
|
+ d\omega_{ij} = \frac{\partial \omega_{ij}}{\partial X_k}dX_k = \omega_{ij,k}.
|
|
|
+$$
|
|
|
+
|
|
|
+
|
|
|
+$$
|
|
|
+ U_i(X'_1,X'_2,X'_3) = U_i^0 + \omega_{ij}^0(X'_j - X_j^0) + \int_{M^0}^{M'}\varepsilon_{ij}dX_j + \int_{M^0}^{M'}(X'_j - X_j^0)d\omega_{ij}.
|
|
|
+$$
|
|
|
+
|
|
|
+В соответствии с соотношением (\ref{c1:epsilon_alpha_beta_gamma}) можно записать:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:omega_ijk}
|
|
|
+ \omega_{ij,k} = \varepsilon_{ik,j} - \varepsilon_{jk,i}.
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+Выражение (\ref{c1:omega_ijk}) также легко доказывается с использованием соотношений Коши для тензора деформаций $\varepsilon_{ij}$ и формулы для тензора малых вращений, связывающей его с перемещениями. Окончательная формула для вычисления перемещений имеет вид:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:movement_end}
|
|
|
+ \begin{array}{ll}
|
|
|
+ U_i(X'_1,X'_2,X'_3) = & U_i^0 + \omega_{ij}^0(X'_j - X_j^0) + \\
|
|
|
+ & \int_{M^0}^{M'}\left[\varepsilon_{ik} + (X'_j - X_j)(\varepsilon_{ik,j} - \varepsilon_{jk,i}) \right]dX_k.
|
|
|
+ \end{array}
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+Формула (\ref{c1:movement_end}) представляет собой окончательное выражение для вычисления поля перемещений по заданному полю деформаций (формула Чезаро). Используемые в формуле (\ref{c1:movement_end}) константы $U_i^0$ (3 константы) и $\omega_{ij}^0$ (3 константы) устанавливаются из условия, вытекающего из способа закрепления тела в пространстве. Если деформируемое тело или материал в пространстве не закреплены, то перемещения по формуле (\ref{c1:movement_end}) могут быть найдены с точностью до констант.
|
|
|
+
|
|
|
+Перемещения $U_i$ в произвольной точке $M'(X'_1, X'_2, X'_3)$ должны быть функциями координат этой точки и не должны зависеть от пути интегрирования $M^0$ --- $M'$. Для этого подинтегральное выражение в формуле (\ref{c1:movement_end}) должно представлять собой полный дифференциал. Из условия полного дифференциала вытекают следующие условия к подынтегральной функции:
|
|
|
+
|
|
|
+\begin{equation}
|
|
|
+ \label{c1:statements}
|
|
|
+ \begin{array}{l}
|
|
|
+ \frac{\partial}{\partial X_l}\left[\varepsilon_{ik} + (X'_j - X_j)(\varepsilon_{ik,j} - \varepsilon_{kj,i})\right] = \\
|
|
|
+ = \frac{\partial}{\partial X_k}\left[\varepsilon_{il} + (X'_j - X_j)(\varepsilon_{il,j} - \varepsilon_{lj,i})\right].
|
|
|
+ \end{array}
|
|
|
+\end{equation}
|
|
|
+
|
|
|
+Формула (\ref{c1:statements}) представляет собой условие независимости интеграла в формуле (\ref{c1:movement_end}) от пути интегрирования и, таким образом, условие однозначного вычисления перемещений по заданному полю деформаций. То есть для того, чтобы воспользоваться формулой (\ref{c1:movement_end}) поле деформаций должно удовлетворять условию (\ref{c1:statements}).
|
|
|
+
|
|
|
+Если в выражении (\ref{c1:statements}) сделать все необходимые преобразования, то будет видно, что (\ref{c1:statements}) полностью совпадает с уравнениями совместности деформаций, записанными в форме (\ref{c1:comp_def_1}), следовательно, для однозначного вычисления перемещений заданное поле деформаций должно быть кинетически допустимым. Поэтому уравнения совместности деформаций называют еще условиями единственности вычисления перемещений по заданному полю деформаций.
|