|
|
@@ -3,160 +3,80 @@
|
|
|
\usepackage[T2A]{fontenc}
|
|
|
\usepackage[utf8]{inputenc}
|
|
|
\usepackage[english, russian]{babel}
|
|
|
-\usepackage{array}
|
|
|
\usetheme{Warsaw}
|
|
|
\setbeamertemplate{caption}[numbered]
|
|
|
-\setbeamerfont{caption}{size=\scriptsize}
|
|
|
|
|
|
% \logo{\includegraphics[width=25pt]{img/pstu_logo}}
|
|
|
-\title[]{Влияние концентраторов напряжений на прочностные и деформационные
|
|
|
-свойства тканых композитов с поликристаллической матрицей}
|
|
|
-\institute[ПНИПУ]{Пермский национальный исследовательский политехнический университет \\Кафедра механики композиционных материалов и конструкций \\
|
|
|
-Комсомольский пр-т, 29, 614990, Пермь, Россия \\
|
|
|
-Тел. / Факс: +7–342–2391294 \\ denis.v.dedkov@gmail.com, rector@pstu.ru}
|
|
|
-\author{Д.~В.~Дедков, \\ научный руководитель: А.~А.~Ташкинов}
|
|
|
-\date{20 мая 2014}
|
|
|
+\title{Концентрация напряжений в слое тканого композита с локальными технологическими дефектами}
|
|
|
+\institute[ПНИПУ]{Пермский национальный исследовательский политехнический университет}
|
|
|
+\author{Д.~В.~Дедков}
|
|
|
+\date{\today}
|
|
|
|
|
|
\begin{document}
|
|
|
|
|
|
\frame{\titlepage}
|
|
|
|
|
|
-\begin{frame} % Цели и задачи
|
|
|
- \frametitle{Цель и задачи}
|
|
|
+\begin{frame}
|
|
|
+ \frametitle{Проблемы, возникающие при производстве тканых КМ}
|
|
|
|
|
|
-\begin{block}{Цель}
|
|
|
- Разработка новых математических моделей, описывающих механическое поведение
|
|
|
-тканых композитов с локальными дефектами при комбинированных нагружениях.
|
|
|
-\end{block}
|
|
|
-
|
|
|
-\begin{block}{Задачи}
|
|
|
+ \begin{block}{Проблемы}
|
|
|
\begin{itemize}
|
|
|
- \item построение твердотельной модели слоя тканого композиционного материала
|
|
|
- с локальными технологическими дефектами;
|
|
|
- \item разработка математической модели механического поведения слоя тканого
|
|
|
- композита при комбинированном пропорциональном нагружении;
|
|
|
- \item определение коэффициентов концентрации напряжений в слое тканого
|
|
|
-композита с локальными технологическими дефектами.
|
|
|
+ \item Возникновение локальных технологических дефектов;
|
|
|
+ \item существенное влияние дефектов на эффективные упругие и прочностные свойства материала;
|
|
|
+ \item обнаружение дефектов только на этапе выходного контроля.
|
|
|
\end{itemize}
|
|
|
-\end{block}
|
|
|
-
|
|
|
-\end{frame}
|
|
|
-
|
|
|
-\begin{frame} % Актуальность
|
|
|
- \frametitle{Актуальность задачи}
|
|
|
-
|
|
|
- \begin{block}{Применение тканых композитов}
|
|
|
- \begin{itemize}
|
|
|
- \item Авиационная и космическая отрасли;
|
|
|
- \item тяжелое и транспортное машиностроение;
|
|
|
- \item энергетика;
|
|
|
- \item химическая и нефтяная промышленность;
|
|
|
- \item строительство.
|
|
|
- \end{itemize}
|
|
|
- \end{block}
|
|
|
-
|
|
|
- \begin{block}{Исследования}
|
|
|
- \begin{itemize}
|
|
|
- \item С.~В.~Ломов (Левинский католический институт, Бельгия);
|
|
|
- \item Ю.~И.~Димитриенко (МГТУ им. Баумана, Россия).
|
|
|
- \end{itemize}
|
|
|
-
|
|
|
- \end{block}
|
|
|
-
|
|
|
-\end{frame}
|
|
|
-
|
|
|
-\begin{frame} % Изготовление тканей, характеристики тканей
|
|
|
- \frametitle{Изготовление тканей}
|
|
|
-
|
|
|
- \begin{block}{Характеристики тканей}
|
|
|
- \begin{itemize}
|
|
|
- \item волокнистый состав;
|
|
|
- \item тип переплетения;
|
|
|
- \item ширина;
|
|
|
- \item толщина;
|
|
|
- \item масса квадратного метра;
|
|
|
- \item число нитей основы и утка на единицу длины (плотность ткани);
|
|
|
- \item разрывная нагрузка и растяжимость (удлинение) при разрыве.
|
|
|
- \end{itemize}
|
|
|
- \end{block}
|
|
|
-
|
|
|
-\end{frame}
|
|
|
-
|
|
|
-\begin{frame} % Изготовление тканей, типы переплетений
|
|
|
- \frametitle{Изготовление тканей}
|
|
|
- \begin{block}{Типы переплетений}
|
|
|
- \begin{figure}
|
|
|
- \includegraphics[width=\linewidth]{img/all_structs}
|
|
|
- \caption{Схемы типов переплетения: а) полотняное, б)
|
|
|
-сатиновое, в) саржевое $2\times2$}
|
|
|
- \end{figure}
|
|
|
\end{block}
|
|
|
-
|
|
|
-\end{frame}
|
|
|
-
|
|
|
-\begin{frame} % Способы уплотнения матрицы
|
|
|
- \frametitle{Формирование матрицы}
|
|
|
-
|
|
|
- \begin{block}{Способы уплотнения матрицы}
|
|
|
+ \centering{$\Downarrow$}
|
|
|
+ \begin{block}{Типичные локальные дефекты}
|
|
|
\begin{itemize}
|
|
|
- \item с использованием газообразных углеводородов (природный газ, метан,
|
|
|
- пропан-бутан, бензол и т.п.);
|
|
|
- \item с использованием жидких углеводородов с большим выходом кокса (пеки,
|
|
|
- смолы);
|
|
|
- \item комбинированный, включающий в себя пропитку пористых каркасов жидкими
|
|
|
- углеводородами, карбонизацию и уплотнение из газовой фазы.
|
|
|
+ \item Разрыв волокна основы;
|
|
|
+ \item разрывы волокон основы и утка;
|
|
|
+ \item внутренняя пора.
|
|
|
\end{itemize}
|
|
|
\end{block}
|
|
|
|
|
|
\end{frame}
|
|
|
|
|
|
-\begin{frame} % Локальные технологические дефекты, пропуск волокна основы
|
|
|
- \frametitle{Локальные технологические дефекты}
|
|
|
-
|
|
|
- \begin{figure}
|
|
|
- \includegraphics[width=\linewidth]{img/defects/d1d2}
|
|
|
- \caption{Пропуск волокна основы а)~с наличием внутренней полости, б)~с
|
|
|
-дополнительным уплотнением материалом связующего}
|
|
|
- \end{figure}
|
|
|
-
|
|
|
-\end{frame}
|
|
|
-
|
|
|
-\begin{frame} % Локальные технологические дефекты, разрывы волокон
|
|
|
- \frametitle{Локальные технологические дефекты}
|
|
|
+\begin{frame}
|
|
|
+ \frametitle{Примеры дефектов}
|
|
|
|
|
|
- \begin{figure}
|
|
|
- \includegraphics[width=0.6\linewidth]{img/defects/d3d6}
|
|
|
- \caption{Разрыв волокна основы а)~с наличием внутренней полости, б)~с
|
|
|
-дополнительным уплотнением материалом связующего}
|
|
|
- \end{figure}
|
|
|
-
|
|
|
- \begin{figure}
|
|
|
- \includegraphics[width=0.6\linewidth]{img/defects/d4d7}
|
|
|
- \caption{Разрыв волокон основы и утка а)~с наличием внутренней полости, б)~с
|
|
|
-дополнительным уплотнением материалом связующего}
|
|
|
- \end{figure}
|
|
|
+\begin{columns}
|
|
|
+ \begin{column}{0.45\textwidth}
|
|
|
+ \begin{figure}
|
|
|
+ \centering{\includegraphics[width=3.5cm]{img/defects/d1}}
|
|
|
+ \caption{Разрыв волокна основы}
|
|
|
+ \end{figure}
|
|
|
+ \end{column}
|
|
|
+ \begin{column}{0.55\textwidth}
|
|
|
+ \begin{figure}
|
|
|
+ \centering{\includegraphics[width=3.5cm]{img/defects/d2}}
|
|
|
+ \caption{Разрыв волокон основы и утка}
|
|
|
+ \end{figure}
|
|
|
+ \end{column}
|
|
|
+\end{columns}
|
|
|
+\begin{center}
|
|
|
+ \begin{figure}
|
|
|
+ \includegraphics[width=4.8cm]{img/defects/d3}
|
|
|
+ \caption{Внутренняя пора}
|
|
|
+ \end{figure}
|
|
|
+\end{center}
|
|
|
|
|
|
\end{frame}
|
|
|
|
|
|
-\begin{frame} % Локальные технологические дефекты, внутренняя пора
|
|
|
- \frametitle{Локальные технологические дефекты}
|
|
|
+\begin{frame}
|
|
|
+ \frametitle{Описание геометрии волокна}
|
|
|
|
|
|
- \begin{figure}
|
|
|
- \includegraphics[width=0.8\linewidth]{img/defects/d41}
|
|
|
- \caption{Внутренняя пора}
|
|
|
- \end{figure}
|
|
|
-
|
|
|
-\end{frame}
|
|
|
+\begin{columns}
|
|
|
|
|
|
-\begin{frame} % Геометрическая модель
|
|
|
- \frametitle{Геометрия искривленных волокон слоя тканого композита}
|
|
|
+ \begin{column}{0.5\textwidth}
|
|
|
|
|
|
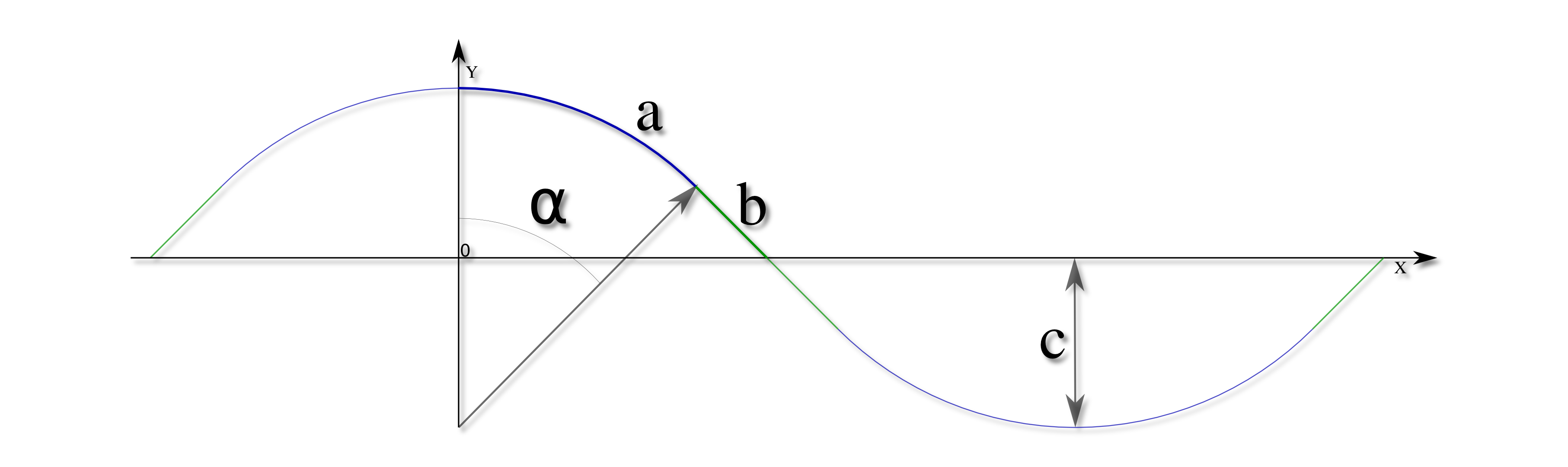
\begin{figure}
|
|
|
- \includegraphics[width=\linewidth]{img/geom1}
|
|
|
- \caption{Участок искривленного волокна}
|
|
|
+ \centering{\includegraphics[width=4.7cm]{img/geom}}
|
|
|
+ \caption{Искривление волокна}
|
|
|
\end{figure}
|
|
|
|
|
|
-\begin{columns}
|
|
|
+ \end{column}
|
|
|
+
|
|
|
\begin{column}{0.5\textwidth}
|
|
|
|
|
|
\begin{block}{Описание геометрии}
|
|
|
@@ -169,11 +89,6 @@
|
|
|
|
|
|
\end{block}
|
|
|
|
|
|
-
|
|
|
- \end{column}
|
|
|
-
|
|
|
- \begin{column}{0.5\textwidth}
|
|
|
-
|
|
|
\begin{block}{Коэффициенты армирования}
|
|
|
$\alpha_{x} = \alpha_{y} = 0.14$
|
|
|
\end{block}
|
|
|
@@ -182,34 +97,35 @@
|
|
|
\end{columns}
|
|
|
\end{frame}
|
|
|
|
|
|
-\begin{frame} % Математическая модель, основные гипотезы
|
|
|
- \frametitle{Математическая модель слоя тканого композита \\ с искривленными волокнами}
|
|
|
+
|
|
|
+\begin{frame}
|
|
|
+ \frametitle{Геометрическая модель слоя тканого композита}
|
|
|
|
|
|
\begin{columns}
|
|
|
- \begin{column}{0.4\textwidth}
|
|
|
+ \begin{column}{0.55\textwidth}
|
|
|
\begin{figure}
|
|
|
- \centering{\includegraphics[width=4.5cm]{img/frame}}
|
|
|
- \caption{Фрагмент слоя тканого композита периодической структуры}
|
|
|
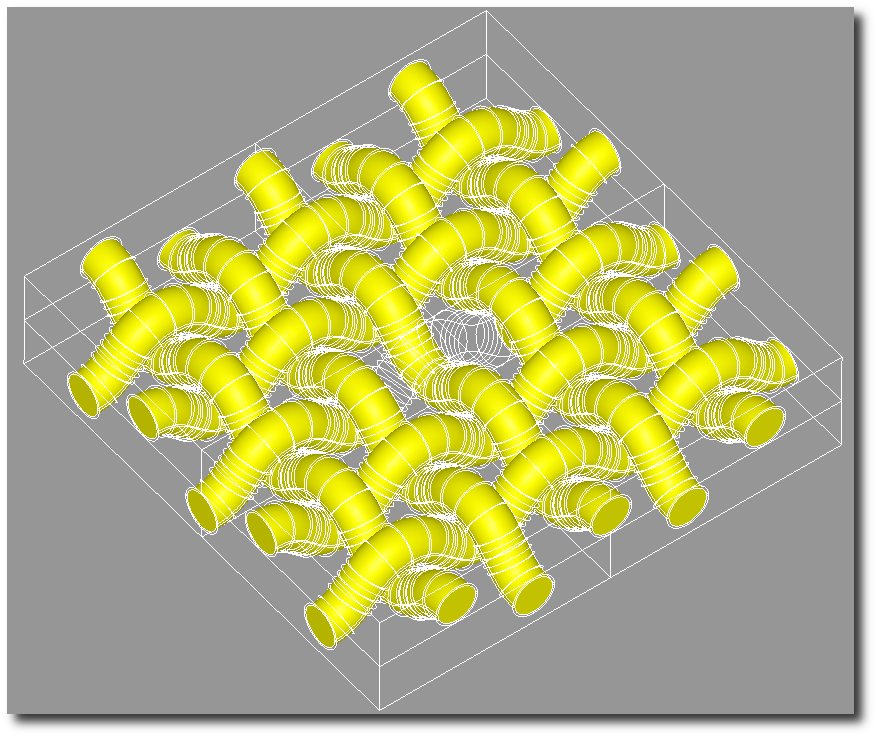
+ \centering{\includegraphics[width=6cm]{img/frame}}
|
|
|
+ \caption{Фрагмент тканого КМ}
|
|
|
\end{figure}
|
|
|
\end{column}
|
|
|
- \begin{column}{0.6\textwidth}
|
|
|
- \begin{footnotesize}
|
|
|
+ \begin{column}{0.45\textwidth}
|
|
|
\begin{block}{Гипотезы}
|
|
|
\begin{itemize}
|
|
|
- \item поликристаллическая матрица изотропна, линейно упруга ($E_m
|
|
|
-= 0.28$ГПа, $\nu_m = 0.4$);
|
|
|
- \item керамические волокна изотропны, линейно упруги ($E_f = 280$ГПа, $\nu_f = 0.2$);
|
|
|
- \item деформации бесконечно малы, взаимное расположение искривленных волокон, места и площади контакта неизменны в процессе нагружения слоя;
|
|
|
- \item волокна окружены гарантированным слоем матрицы (модель 1) или имеют контакт с трением (модель 2)
|
|
|
+ \item матрица изотропная, упругая;
|
|
|
+ \item волокно изотропное, упругое;
|
|
|
+% \item волокна не соприкасаются;
|
|
|
+ \item малые деформации;
|
|
|
+ \item взаимное расположение волокон неизменно,
|
|
|
+ \item задана граница контакта с трением.
|
|
|
\end{itemize}
|
|
|
+
|
|
|
\end{block}
|
|
|
- \end{footnotesize}
|
|
|
\end{column}
|
|
|
\end{columns}
|
|
|
\end{frame}
|
|
|
|
|
|
-\begin{frame} % Математическая модель, краевая задача
|
|
|
- \frametitle{Математическая модель слоя тканого композита \\ с искривленными волокнами}
|
|
|
+\begin{frame}
|
|
|
+ \frametitle{Краевая задача}
|
|
|
|
|
|
\begin{block}{Уравнения равновесия в напряжениях}
|
|
|
$$\sigma_{ij,j} ({\bf r}) = 0;$$
|
|
|
@@ -224,7 +140,7 @@
|
|
|
\lambda =
|
|
|
\left\{
|
|
|
\begin{array}{l}
|
|
|
- 1, {\bf r} \in V_f; \\
|
|
|
+ 1, {\bf r} \in V_f \\
|
|
|
0, {\bf r} \in V_m
|
|
|
\end{array}
|
|
|
\right.
|
|
|
@@ -243,10 +159,11 @@
|
|
|
|
|
|
\end{frame}
|
|
|
|
|
|
-\begin{frame} % Математическая модель, граничные условия
|
|
|
+
|
|
|
+\begin{frame}
|
|
|
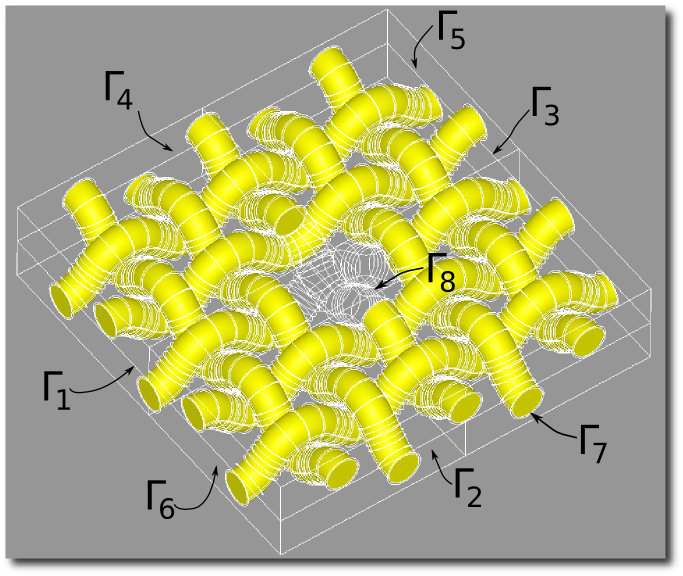
\frametitle{Граничные условия}
|
|
|
|
|
|
- \begin{block}{Двухосное равнокомпонентное растяжение}
|
|
|
+ \begin{block}{Граничные условия}
|
|
|
\begin{itemize}
|
|
|
\item $u_1 {\bf (r)}|_{\Gamma_2} = u_1^0;$
|
|
|
$u_3 {\bf (r)}|_{\Gamma_1} = u_3^0;$
|
|
|
@@ -261,7 +178,7 @@
|
|
|
|
|
|
\begin{columns}
|
|
|
\begin{column}{0.6\textwidth}
|
|
|
- \begin{block}{Идеальное сопряжение на межфазных поверхностях}
|
|
|
+ \begin{block}{Условия идеального сопряжения}
|
|
|
\begin{itemize}
|
|
|
\item $\left[\sigma_{ij}({\bf r})n_{j}({\bf r})\right]|_{\Gamma_7^+} =
|
|
|
\left[\sigma_{ij}({\bf r})n_{j}({\bf r})\right]|_{\Gamma_7^-}$
|
|
|
@@ -275,6 +192,11 @@
|
|
|
\item $\left[\sigma_{ij}({\bf r})n_j({\bf r})\right]_{\Gamma_8} = 0$
|
|
|
\end{itemize}
|
|
|
\end{block}
|
|
|
+% \begin{block}{Условие контакта с трением}
|
|
|
+% \begin{itemize}
|
|
|
+% \item $\sigma_{12}({\bf r}) \geq f \sigma_{12}^k({\bf r})$
|
|
|
+% \end{itemize}
|
|
|
+% \end{block}
|
|
|
\end{column}
|
|
|
\begin{column}{0.4\textwidth}
|
|
|
\includegraphics[width=1\linewidth]{img/gu}
|
|
|
@@ -282,112 +204,82 @@
|
|
|
\end{columns}
|
|
|
\end{frame}
|
|
|
|
|
|
-\begin{frame} % Математическая модель, условия контакта
|
|
|
- \frametitle{Граничные условия}
|
|
|
-
|
|
|
- \begin{block}{Контакт между волокнами основы и утка}
|
|
|
- если $\left[\sigma_{n\tau} {\bf (r)} \right] |_{\Gamma_9^{+}} <
|
|
|
- \left[ f | \sigma_{nn} {\bf (r)} | \right] |_{\Gamma_9^{-}}$, то
|
|
|
- $$
|
|
|
- \left[\sigma_{n\tau} {\bf (r)} n_{n} \right] |_{\Gamma_9^{+}} =
|
|
|
- \left[\sigma_{n\tau} {\bf (r)} n_{n} \right] |_{\Gamma_9^{-}}, \quad
|
|
|
- \left[u_n {\bf (r)}\right]|_{\Gamma_9^{+}} = \left[u_n {\bf
|
|
|
- (r)}\right]|_{\Gamma_9^{-}} ,
|
|
|
- $$
|
|
|
- \noindent а, если $\left[\sigma_{n\tau} {\bf (r)} \right] |_{\Gamma_9^{+}} \geq
|
|
|
- \left[ f | \sigma_{nn} {\bf (r)} | \right] |_{\Gamma_9^{-}}$, то
|
|
|
- $$
|
|
|
- \left[\sigma_{n\tau} {\bf (r)} \right] |_{\Gamma_9^{+}} \geq
|
|
|
- \left[ f | \sigma_{nn} {\bf (r)} | \right] |_{\Gamma_9^{-}}, \quad
|
|
|
- \left[u_n {\bf (r)}\right]|_{\Gamma_9^{+}} = \left[u_n {\bf
|
|
|
- (r)}\right]|_{\Gamma_9^{-}} ,
|
|
|
- $$
|
|
|
- \noindent где индексы $n$ и $\tau$ --- определяют направление внешней нормали и касательной к поверхности $\Gamma_9$.
|
|
|
- \end{block}
|
|
|
-
|
|
|
+\begin{frame}
|
|
|
+ \frametitle{Условия контакта с трением}
|
|
|
+
|
|
|
+ если $\left[\sigma_{n\tau} {\bf (r)} \right] |_{\Gamma_9^{+}} <
|
|
|
+\left[ f | \sigma_{nn} {\bf (r)} | \right] |_{\Gamma_9^{-}}$, то
|
|
|
+$$
|
|
|
+\left[\sigma_{n\tau} {\bf (r)} n_{n} \right] |_{\Gamma_9^{+}} =
|
|
|
+\left[\sigma_{n\tau} {\bf (r)} n_{n} \right] |_{\Gamma_9^{-}}, \quad
|
|
|
+\left[u_n {\bf (r)}\right]|_{\Gamma_9^{+}} = \left[u_n {\bf
|
|
|
+(r)}\right]|_{\Gamma_9^{-}} ,
|
|
|
+$$
|
|
|
+\noindent а, если $\left[\sigma_{n\tau} {\bf (r)} \right] |_{\Gamma_9^{+}} \geq
|
|
|
+\left[ f | \sigma_{nn} {\bf (r)} | \right] |_{\Gamma_9^{-}}$, то
|
|
|
+$$
|
|
|
+\left[\sigma_{n\tau} {\bf (r)} \right] |_{\Gamma_9^{+}} \geq
|
|
|
+\left[ f | \sigma_{nn} {\bf (r)} | \right] |_{\Gamma_9^{-}}, \quad
|
|
|
+\left[u_n {\bf (r)}\right]|_{\Gamma_9^{+}} = \left[u_n {\bf
|
|
|
+(r)}\right]|_{\Gamma_9^{-}} ,
|
|
|
+$$
|
|
|
+\noindent где индексы $n$ и $\tau$ --- определяют направление внешней нормали и касательной к поверхности $\Gamma_9$.
|
|
|
|
|
|
\end{frame}
|
|
|
|
|
|
-\begin{frame} % Используемое ПО
|
|
|
- \frametitle{Используемое программное обеспечение}
|
|
|
|
|
|
- \begin{block}{Некоммерческая платформа численного моделирования SALOME-MECA}
|
|
|
+\begin{frame}
|
|
|
+ \frametitle{Используемое ПО}
|
|
|
+
|
|
|
+ \begin{block}{SALOME}
|
|
|
\begin{itemize}
|
|
|
- \item Доступность для различных ОС;
|
|
|
- \item открытый исходный код;
|
|
|
- \item расширение пользовательскими модулями на языке Python;
|
|
|
- \item возможность параллельных вычислений.
|
|
|
+ \item Создание и редактирование геометрических моделей;
|
|
|
+ \item создание, редактирование, проверка качества конечно-элементной сетки;
|
|
|
+ \item задание физических свойств геометрическим элементам;
|
|
|
+ \item выполнение вычислений с помощью внешних решателей;
|
|
|
+ \item просмотр результатов вычислений.
|
|
|
\end{itemize}
|
|
|
\end{block}
|
|
|
|
|
|
- \begin{block}{Встраиваемая СУБД SQLite}
|
|
|
+ \begin{block}{Code-Aster}
|
|
|
\begin{itemize}
|
|
|
- \item Отсутствие необходимости установки серверной части СУБД;
|
|
|
- \item высокая скорость работы с большими объемами данных.
|
|
|
+ \item Статические, квазистатические, линейные или нелинейные;
|
|
|
+ \item динамические линейные или нелинейные;
|
|
|
+ \item задачи разрушения и усталости.
|
|
|
\end{itemize}
|
|
|
+
|
|
|
\end{block}
|
|
|
|
|
|
\end{frame}
|
|
|
|
|
|
-\begin{frame} % Конечноэлементная модель
|
|
|
- \frametitle{Конечноэлементная модель}
|
|
|
+\begin{frame}
|
|
|
+ \frametitle{Конечно-элементная модель}
|
|
|
+
|
|
|
+ \begin{columns}
|
|
|
+ \begin{column}{0.5\textwidth}
|
|
|
+ \begin{figure}
|
|
|
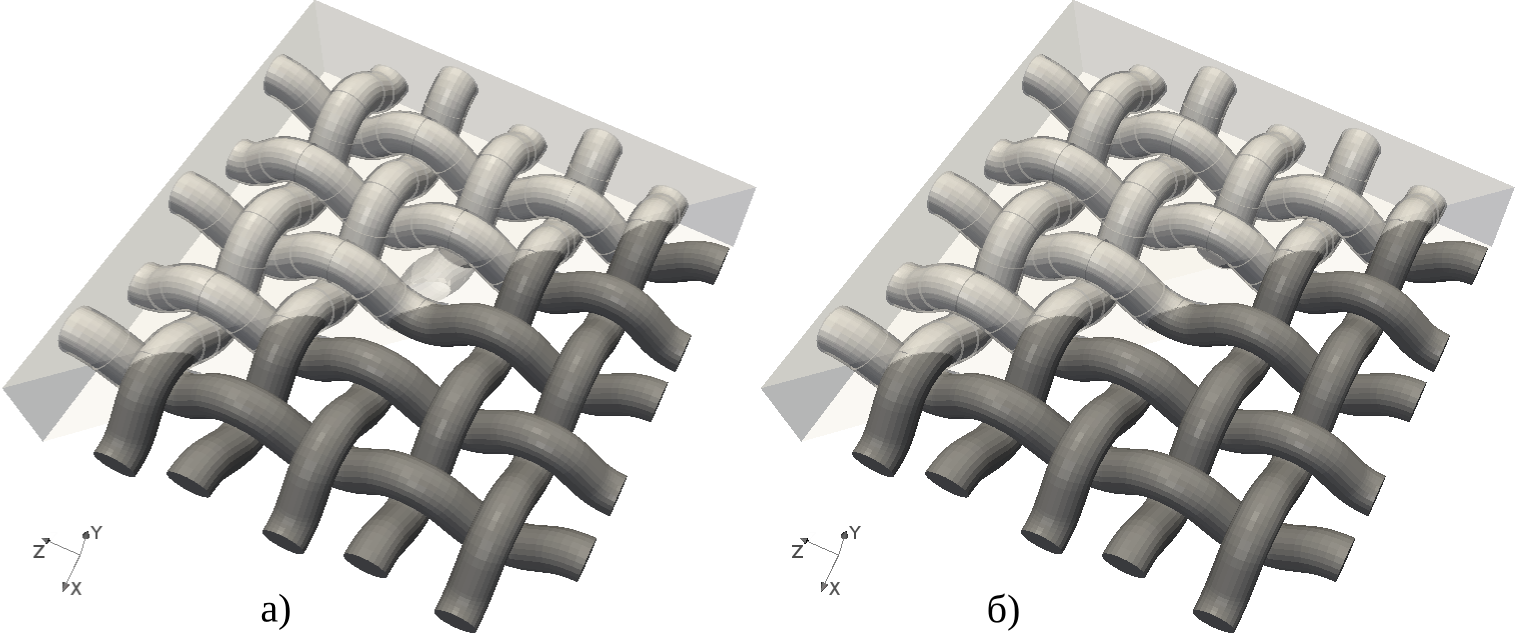
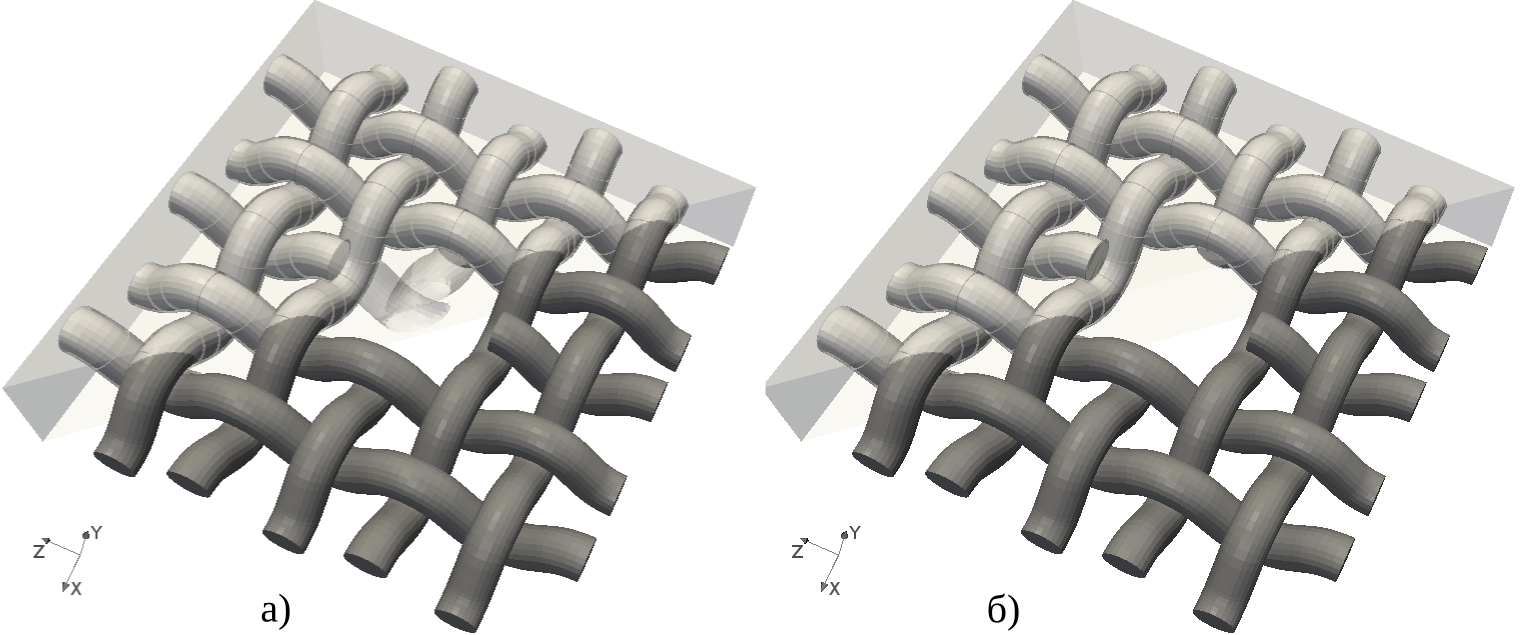
+ \centering{\includegraphics[width=0.7\linewidth]{img/meshes/all}}
|
|
|
+ \caption{Фрагмент слоя тканого КМ}
|
|
|
+ \end{figure}
|
|
|
+ \end{column}
|
|
|
+ \begin{column}{0.5\textwidth}
|
|
|
+ \begin{figure}
|
|
|
+ \centering{\includegraphics[width=0.65\linewidth]{img/meshes/fibers}}
|
|
|
+ \caption{Волокна}
|
|
|
+ \end{figure}
|
|
|
+ \end{column}
|
|
|
+ \end{columns}
|
|
|
|
|
|
\begin{figure}
|
|
|
- \centering{\includegraphics[width=0.6\linewidth]{img/meshes/all}}
|
|
|
- \caption{Топология конечноэлементной сетки волокон (a) и матрицы (b)}
|
|
|
+ \centering{\includegraphics[width=0.45\linewidth]{img/meshes/matrix}}
|
|
|
+ \caption{Сгущение сетки}
|
|
|
\end{figure}
|
|
|
|
|
|
\end{frame}
|
|
|
|
|
|
-\begin{frame} % Тестирование модели
|
|
|
- \frametitle{Тестирование модели}
|
|
|
-
|
|
|
- \begin{table}
|
|
|
- \caption{Зависимость интенсивностей напряжений от количества конечных
|
|
|
-элементов (дефект 1 --- туннельная пора, дефект 2 --- туннельная пора с
|
|
|
-дополнительным уплотнением)}
|
|
|
-
|
|
|
- \begin{tabular}{|c|c||c|c||c|c|}
|
|
|
- \hline
|
|
|
- \multicolumn{2}{|p{2.2cm}||}{Без дефекта}&
|
|
|
- \multicolumn{2}{|p{2.2cm}||}{Дефект 1}&
|
|
|
- \multicolumn{2}{|p{2.2cm}| }{Дефект 2} \\
|
|
|
- \hline
|
|
|
- $C$ & $\sigma_{I}$ & $C$ & $\sigma_{I}$ & $C$ & $\sigma_{I}$ \\
|
|
|
- \hline
|
|
|
- \hline
|
|
|
- 218 207 & 33.6 & 213 381 & 38.0 & 194 196 & 37.9 \\
|
|
|
- \hline
|
|
|
- 271 644 & 32.0 & 261 695 & 36.2 & 241 932 & 36.0 \\
|
|
|
- \hline
|
|
|
- 365 283 & 31.1 & 345 396 & 35.2 & 326 327 & 35.2 \\
|
|
|
- \hline
|
|
|
- 427 855 & 31.2 & 402 304 & 35.4 & 382 954 & 35.3 \\
|
|
|
- \hline
|
|
|
- \end{tabular}
|
|
|
-\end{table}
|
|
|
-
|
|
|
- \begin{table}
|
|
|
- \caption{Зависимость времени рассчетов от числа ядер процессора (относительно
|
|
|
-рассчета на одном ядре)}
|
|
|
-
|
|
|
- \begin{tabular}{|c||c|c|c|}
|
|
|
- \hline
|
|
|
- Кол-во ядер & Без дефекта & Дефект 1 & Дефект 2 \\
|
|
|
- \hline
|
|
|
- \hline
|
|
|
- 2 & 0.62 & 0.60 & 0.62 \\
|
|
|
- \hline
|
|
|
- 4 & 0.40 & 0.43 & 0.41 \\
|
|
|
- \hline
|
|
|
- \end{tabular}
|
|
|
-\end{table}
|
|
|
-
|
|
|
-\end{frame}
|
|
|
-
|
|
|
-\begin{frame} % Топология конечноэлементной сетки
|
|
|
- \frametitle{Топология конечноэлементной сетки}
|
|
|
- \begin{block}{Модель 1: волокна окружены гарантированным слоем матрицы}
|
|
|
+\begin{frame}
|
|
|
+ \frametitle{Топология конечно-элементной сетки}
|
|
|
+ \begin{block}{Модель без учёта трения}
|
|
|
\begin{center}
|
|
|
\begin{footnotesize}
|
|
|
\begin{tabular}{l||c|c}
|
|
|
@@ -398,8 +290,6 @@
|
|
|
\hline
|
|
|
Идеальная структура & 298~255 & 77~760 \\
|
|
|
\hline
|
|
|
- Туннельная пора & 285~664 & 69~984 \\
|
|
|
- \hline
|
|
|
Разрыв волокна основы & 285~466 & 75~168 \\
|
|
|
\hline
|
|
|
Разрыв волокон основы и утка & 279~276 & 72~576 \\
|
|
|
@@ -411,7 +301,7 @@
|
|
|
\end{center}
|
|
|
\end{block}
|
|
|
|
|
|
- \begin{block}{Модель 2: волокна основы и утка имеют контакт с трением}
|
|
|
+ \begin{block}{Модель с учётом трения}
|
|
|
\begin{center}
|
|
|
\begin{footnotesize}
|
|
|
\begin{tabular}{l||c|c}
|
|
|
@@ -433,149 +323,90 @@
|
|
|
|
|
|
\end{frame}
|
|
|
|
|
|
-\begin{frame} % Поля напряжений
|
|
|
- \frametitle{Поля напряжений в элементах структуры}
|
|
|
+
|
|
|
+\begin{frame}
|
|
|
+ \frametitle{Поля напряжений}
|
|
|
|
|
|
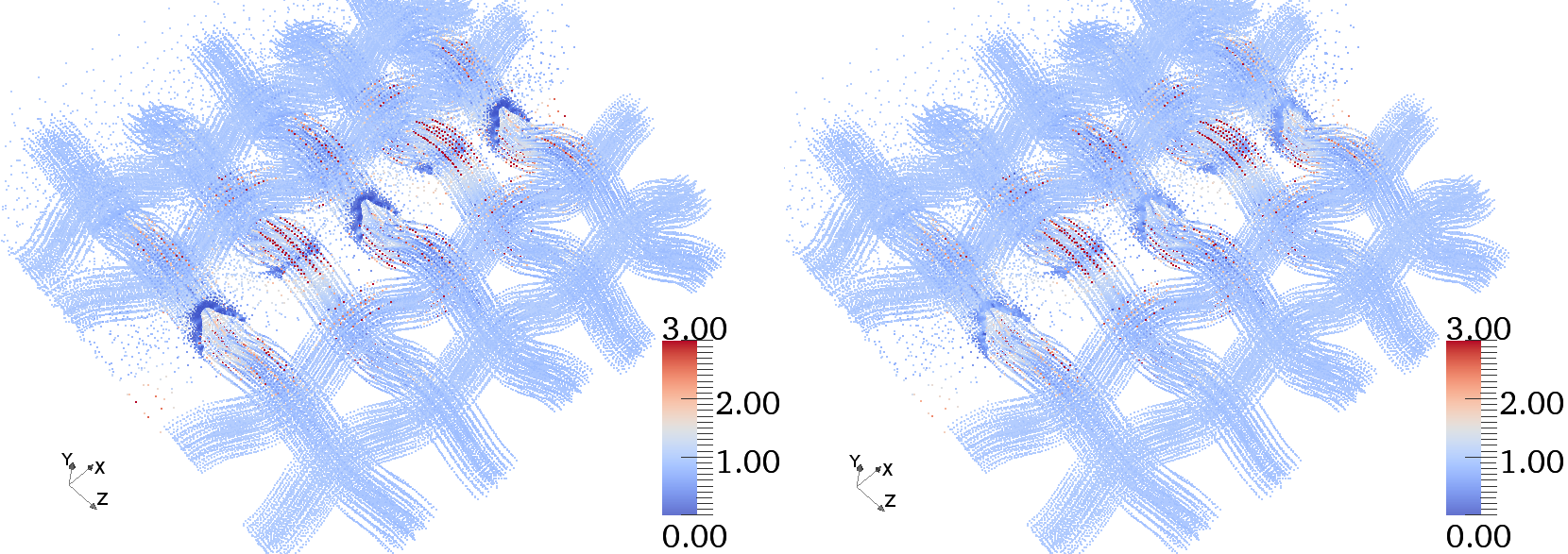
\begin{figure}
|
|
|
- \centering{\includegraphics[width=0.9\linewidth]{img/fields/vmis}}
|
|
|
- \caption{Поля интенсивности напряжений (ГПа) в волокнах основы и утка (композит идеальной периодической структуры)}
|
|
|
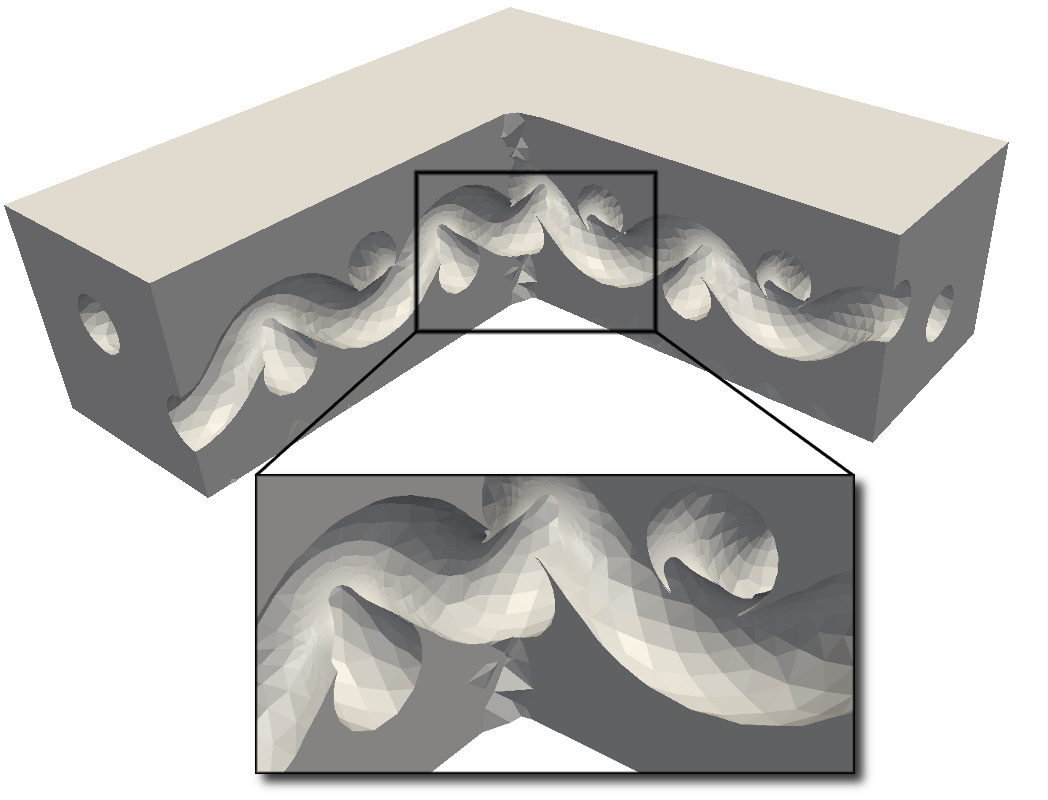
+ \centering{\includegraphics[width=\linewidth]{img/fields/vmis}}
|
|
|
+ \caption{Поля интенсивности напряжений в идеальной периодической структуре}
|
|
|
\end{figure}
|
|
|
|
|
|
\end{frame}
|
|
|
|
|
|
-\setlength{\extrarowheight}{2pt}
|
|
|
-
|
|
|
-\begin{frame} % Коэффициенты концентрации, двухосное растяжение
|
|
|
- \frametitle{Максимальные безразмерные коэффициенты концентрации напряжений
|
|
|
-при двухосном равнокомпонентном растяжении}
|
|
|
- \begin{block}{Модель 1: волокна окружены гарантированным слоем матрицы}
|
|
|
+\begin{frame}
|
|
|
+ \frametitle{Максимальные коэффициенты концентрации напряжений}
|
|
|
+ \begin{block}{Без учёта трения}
|
|
|
\begin{center}
|
|
|
- \begin{footnotesize}
|
|
|
+ \begin{scriptsize}
|
|
|
\input{s_max_table_all_res}
|
|
|
- \end{footnotesize}
|
|
|
+ \end{scriptsize}
|
|
|
\end{center}
|
|
|
\end{block}
|
|
|
-
|
|
|
- \begin{block}{Модель 2: волокна основы и утка имеют контакт с трением}
|
|
|
- \begin{center}
|
|
|
- \begin{footnotesize}
|
|
|
- \input{s_max_table_all_res_fr}
|
|
|
- \end{footnotesize}
|
|
|
- \end{center}
|
|
|
- \end{block}
|
|
|
-
|
|
|
-\end{frame}
|
|
|
|
|
|
-\begin{frame} % Коэффициенты концентрации, чистое формоизменение
|
|
|
- \frametitle{Максимальные безразмерные коэффициенты концентрации напряжений при
|
|
|
-чистом формоизменении}
|
|
|
-
|
|
|
- \begin{block}{Модель 1: волокна окружены гарантированным слоем матрицы}
|
|
|
- \begin{center}
|
|
|
- \begin{footnotesize}
|
|
|
- \input{s_max_table_all_res_s2}
|
|
|
- \end{footnotesize}
|
|
|
- \end{center}
|
|
|
- \end{block}
|
|
|
-
|
|
|
- \begin{block}{Модель 2: волокна основы и утка имеют контакт с трением}
|
|
|
+ \begin{block}{С учётом трения}
|
|
|
\begin{center}
|
|
|
- \begin{footnotesize}
|
|
|
- \input{s_max_table_all_res_fr_s2}
|
|
|
- \end{footnotesize}
|
|
|
+ \begin{scriptsize}
|
|
|
+ \input{s_max_table_all_res_fr}
|
|
|
+ \end{scriptsize}
|
|
|
\end{center}
|
|
|
\end{block}
|
|
|
-
|
|
|
-\end{frame}
|
|
|
|
|
|
-\begin{frame} % Коэффициенты концентрации, всестороннее сжатие
|
|
|
- \frametitle{Максимальные безразмерные коэффициенты концентрации напряжений при
|
|
|
-деформации всестороннего сжатия}
|
|
|
-
|
|
|
- \begin{block}{Модель 1: волокна окружены гарантированным слоем матрицы}
|
|
|
- \begin{center}
|
|
|
- \begin{footnotesize}
|
|
|
- \input{s_max_table_all_res_s3}
|
|
|
- \end{footnotesize}
|
|
|
- \end{center}
|
|
|
- \end{block}
|
|
|
-
|
|
|
- \begin{block}{Модель 2: волокна основы и утка имеют контакт с трением}
|
|
|
- \begin{center}
|
|
|
- \begin{footnotesize}
|
|
|
- \input{s_max_table_all_res_fr_s3}
|
|
|
- \end{footnotesize}
|
|
|
- \end{center}
|
|
|
- \end{block}
|
|
|
-
|
|
|
\end{frame}
|
|
|
|
|
|
-\begin{frame} % Коэффициенты интенсивностей напряжений, модель 1
|
|
|
- \frametitle{Безразмерные коэффициенты концентрации интенсивности напряжений. Модель 1: волокна окружены гарантированным слоем матрицы}
|
|
|
+\begin{frame}
|
|
|
+ \frametitle{Коэффициенты концентрации интенсивности напряжений без учёта трения}
|
|
|
|
|
|
- \begin{figure}
|
|
|
- \centering{\includegraphics[width=\linewidth]{img/fields/s0d5d6}}
|
|
|
- \caption{Разрыв волокон основы и утка основы}
|
|
|
- \end{figure}
|
|
|
+ \begin{columns}
|
|
|
+ \begin{column}{0.5\textwidth}
|
|
|
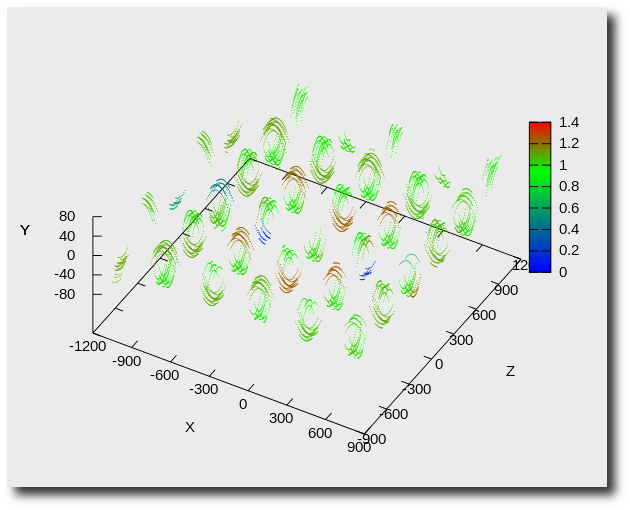
+ \begin{figure}
|
|
|
+ \centering{\includegraphics[width=\linewidth]{img/fields/d3_k}}
|
|
|
+ \caption{Разрыв волокна основы}
|
|
|
+ \end{figure}
|
|
|
+ \end{column}
|
|
|
+ \begin{column}{0.5\textwidth}
|
|
|
+ \begin{figure}
|
|
|
+ \centering{\includegraphics[width=\linewidth]{img/fields/d4_k}}
|
|
|
+ \caption{Разрыв волокон основы и утка}
|
|
|
+ \end{figure}
|
|
|
+ \end{column}
|
|
|
+ \end{columns}
|
|
|
\end{frame}
|
|
|
|
|
|
-\begin{frame} % Коэффициенты интенсивностей напряжений, модель 2
|
|
|
- \frametitle{Безразмерные коэффициенты концентрации интенсивности напряжений. Модель 2: волокна основы \\ и утка имеют контакт с трением}
|
|
|
+\begin{frame}
|
|
|
+ \frametitle{Коэффициенты концентрации интенсивности напряжений с учётом трения}
|
|
|
|
|
|
+ \begin{columns}
|
|
|
+ \begin{column}{0.5\textwidth}
|
|
|
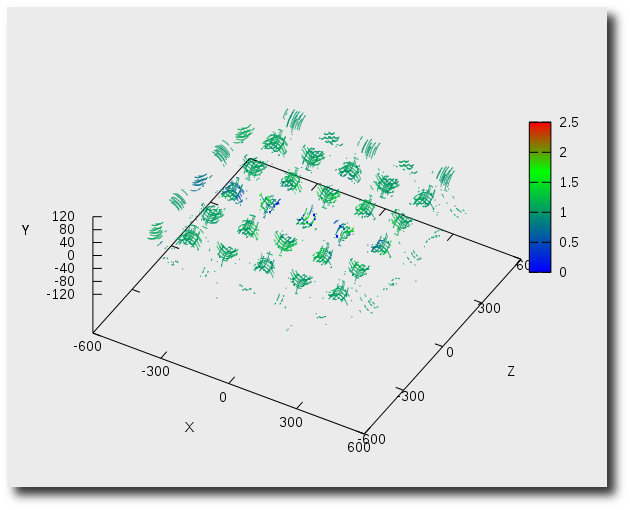
+ \begin{figure}
|
|
|
+ \centering{\includegraphics[width=\linewidth]{img/fields/d3_k_fric}}
|
|
|
+ \caption{Разрыв волокна основы}
|
|
|
+ \end{figure}
|
|
|
+ \end{column}
|
|
|
+ \begin{column}{0.5\textwidth}
|
|
|
\begin{figure}
|
|
|
- \centering{\includegraphics[width=\linewidth]{img/fields/d1d2}}
|
|
|
- \caption{Пропуск волокна основы}
|
|
|
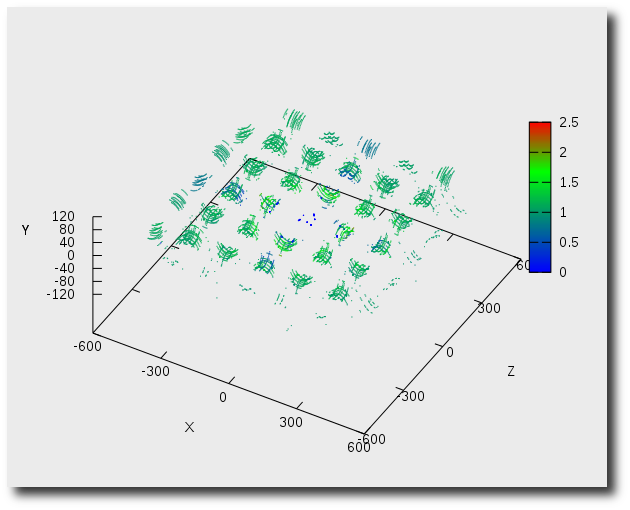
+ \centering{\includegraphics[width=\linewidth]{img/fields/d4_k_fric}}
|
|
|
+ \caption{Разрыв волокон основы и утка}
|
|
|
\end{figure}
|
|
|
+ \end{column}
|
|
|
+ \end{columns}
|
|
|
\end{frame}
|
|
|
|
|
|
-\begin{frame} % Выводы
|
|
|
+\begin{frame}
|
|
|
\frametitle{Выводы}
|
|
|
|
|
|
- \begin{block}{}
|
|
|
- \begin{footnotesize}
|
|
|
+ \begin{block}{Мероприятия для повышения способности тканых КМ сопротивляться внешнему силовому воздействию}
|
|
|
\begin{itemize}
|
|
|
- \item Разработана и протестирована математическая модель слоя тканого
|
|
|
-композита с искривленными волокнами и поликристаллической матрицей;
|
|
|
- \item разработан модуль расширения платформы численного моделирования
|
|
|
-SALOME-MECA для вычисления коэффициентов концентрации напряжений;
|
|
|
- \item при различных видах внешнего нагружения на основе численного решения
|
|
|
-краевых задач методом конечных элементов определены коэффициенты
|
|
|
-концентрации напряжений, вызванные наличием локальных технологических
|
|
|
-дефектов;
|
|
|
- \item установлено что механизмы, инициирующие разрушение
|
|
|
-поликристаллической матрицы, могут различаться, в зависимости от вида внешней
|
|
|
-нагрузки.
|
|
|
+ \item Операции технологического процесса, обеспечивающие проникновение связующего в полости локальных дефектов;
|
|
|
+ \item дополнительная пропитка связующим, доуплотнение, карбонизация, доосаждение матрицы из газовой фазы.
|
|
|
\end{itemize}
|
|
|
- \end{footnotesize}
|
|
|
+
|
|
|
\end{block}
|
|
|
|
|
|
\end{frame}
|
|
|
|
|
|
-\begin{frame} % Публикации
|
|
|
- \frametitle{Публикации}
|
|
|
-
|
|
|
-\begin{footnotesize}
|
|
|
- \begin{itemize}
|
|
|
- \item Дедков~Д.~В., Зайцев~А.~В., Ташкинов~А.~А. Концентрация напряжений в
|
|
|
-слое тканого композита с закрытыми внутренними технологическими порами. //
|
|
|
-Вестник ПНИПУ. Механика, --- 2011. --- Т.4, --- № 4, с. 29--36 (с 2013 г.
|
|
|
-входит в базы цитирования Scopus).
|
|
|
-
|
|
|
- \item Дедков~Д.~В., Зайцев~А.~В. Концентрация напряжений в слое тканого
|
|
|
-композита с локальными дефектами при двухосном однородном равнокомпонентном
|
|
|
-макродеформировании // Вестник Сам. гос. техн. ун-та. Сер. Физ.-мат. науки.,
|
|
|
---- 2013, --- № 4, с. 66--75.
|
|
|
-
|
|
|
- \item Дедков~Д.~В., Ташкинов~А.~А. Коэффициенты концентрации напряжений в
|
|
|
-слое тканого композита с локальными технологическими дефектами при чистом
|
|
|
-формоизменении // Вычислительная механика сплошных сред., --- 2013 --- Т.6, ---
|
|
|
-№1., --- с. 103--109 (входит в базы цитирования WOS и Scopus)
|
|
|
- \end{itemize}
|
|
|
-\end{footnotesize}
|
|
|
-
|
|
|
-\end{frame}
|
|
|
|
|
|
-\begin{frame} % Спасибо за внимание
|
|
|
+\begin{frame}
|
|
|
\begin{block}{}
|
|
|
\centering{Спасибо за внимание!}
|
|
|
\end{block}
|